中学受験の算数で出題される単元「つるかめ算」。中学受験をしようと考えている人は一度は聞いたことのある言葉だと思います。つるかめ算は数ある中学受験の算数の中でも対策として度々名が上がる問題です。
中学受験では出題されますが、学校の教科書には載っておらず、授業も行われません。ここの部分が受験生にとって悩みの種となります。特殊な問題で解き方が理解できていない場合、大変苦戦する単元です。
この記事では、理解が難しいつるかめ算をわかりやすく解説しています。算数が苦手な人やつるかめ算を初めて学習する人、つるかめ算が理解できない人でも理解できる内容となっています。この記事を読むことでつるかめ算の計算方法が理解でき、つるかめ算で悩むことはありません。
中学受験は算数や国語ではなく、「社会」の出来で合否が決まります!
そのため、第一志望に合格したいのであれば、社会を家庭学習でまず最初に固めるのが断トツの近道です!
【社会を最初に固めるべき理由】
● 算数の1点と社会の1点は、総合点で考えれば同じ1点
● 社会は暗記教科で学習センスがいらない!
● 社会は塾任せでは絶対に伸びない、家庭学習で伸ばす!
【短期間で社会の偏差値を上げたい方必見!】
短期間で偏差値を10以上アップさせた受験生多数!社会の偏差値を最速でアップできる社会に特化したスーパー教材を下記のページでご紹介しています!
\ 30日で社会の偏差値がアップ! /
スタディアップの教材はこちら
【たった5分で丸わかり】
つるかめ算① つるかめ算とは
つるかめ算とは、つるとかめのように、足数が異なるものがあって、足数の合計と頭数の合計がわかっているときに、つるとかめのそれぞれの頭数を求める問題のことを言います。
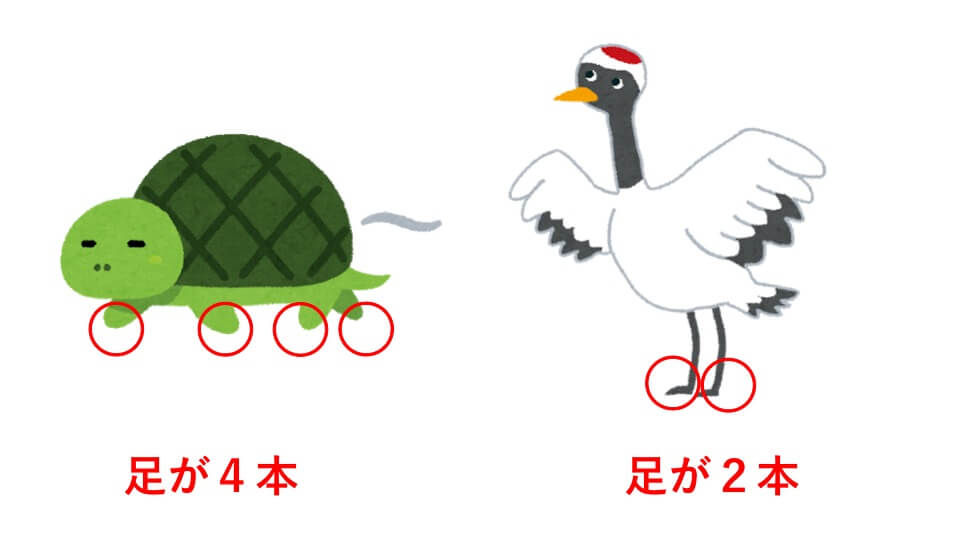
上の図のようにつるの足は2本、かめの足は4本あります。
つるとかめが何匹かいるときに、全部がつるであると仮定(仮として考える)したり、全部がかめであると仮定することで、実際の違いから、つるとかめのそれぞれの頭数を求めます。
詳しいやり方は基本問題を使って解説していきます。
つるかめ算② 基本問題
例題1
つるとかめが合わせて8匹います。このときの足数が22本のとき、つるとかめは何匹いますか?
解説
つるとかめが合わせて8匹いるということは頭数が8ということです。頭数と足数がわかっているので、全部つるだと仮定したときの足数と実際の足数の違いから、かめの数を求めます。
8匹全部つるとしたときの足数は
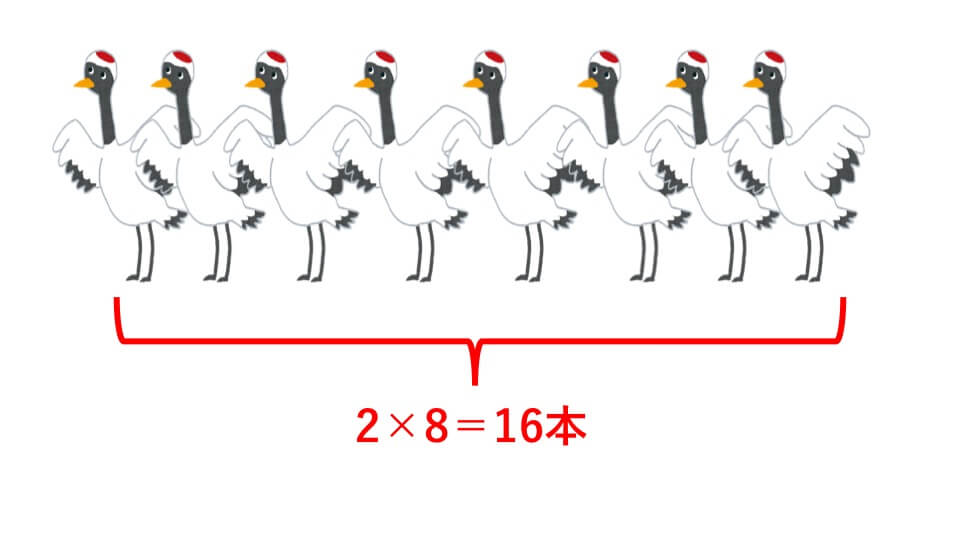
上の図のように16本となります。実際の足の数は22本なので、その差を求めると
22-16=6(本)となります。
つる1匹をかめ1匹に置き換えると、足の数は
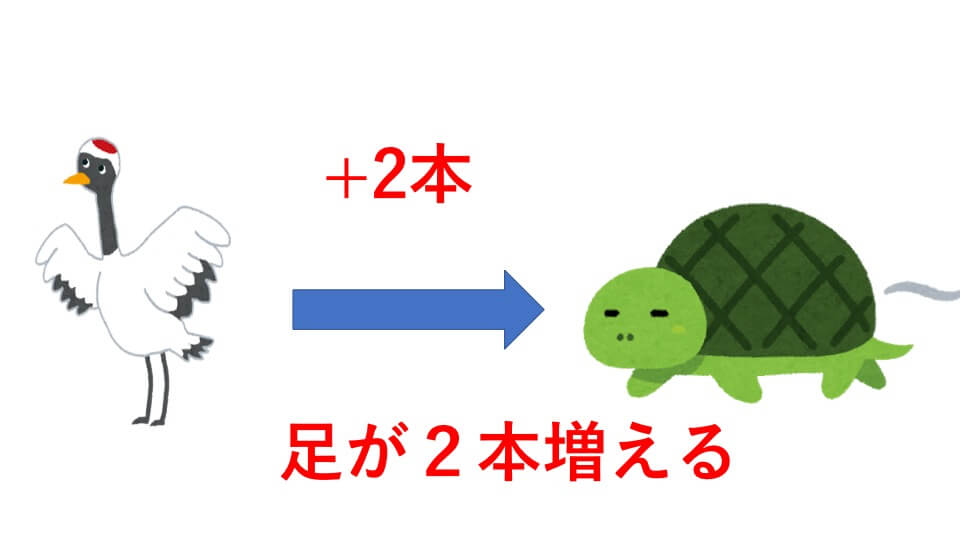
上の図のようになり2本増えることがわかります。
足の数を6本増やすと合計22本になるので、つるをかめに置き換える数は、
6÷2=3(匹)
つるの数は
8-3=5(匹)
よって答えつる5匹 かめ3匹
*本来つるの数え方は羽(わ)ですが、ここではわかりやすいように匹を使っています。
例題2
パトカーと白バイが合わせて7台あります。タイヤの数の合計は20本です。パトカーと白バイはそれぞれ何台ありますか?
解説
まずパトカーのタイヤの数は4本、白バイのタイヤの数は2本ということを理解してください。
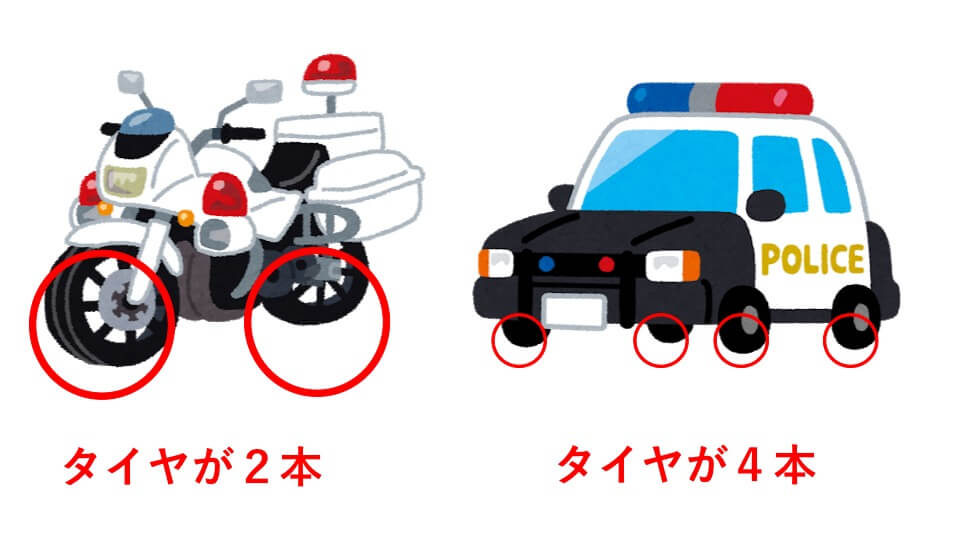
ここで7台全部がパトカーだと考えると、タイヤの数は
4×7=28(本)となります。実際のタイヤの数は20本なので、その差を求めると
28-20=8(本)となります。パトカー1台を白バイ1台に変えるとタイヤの数は
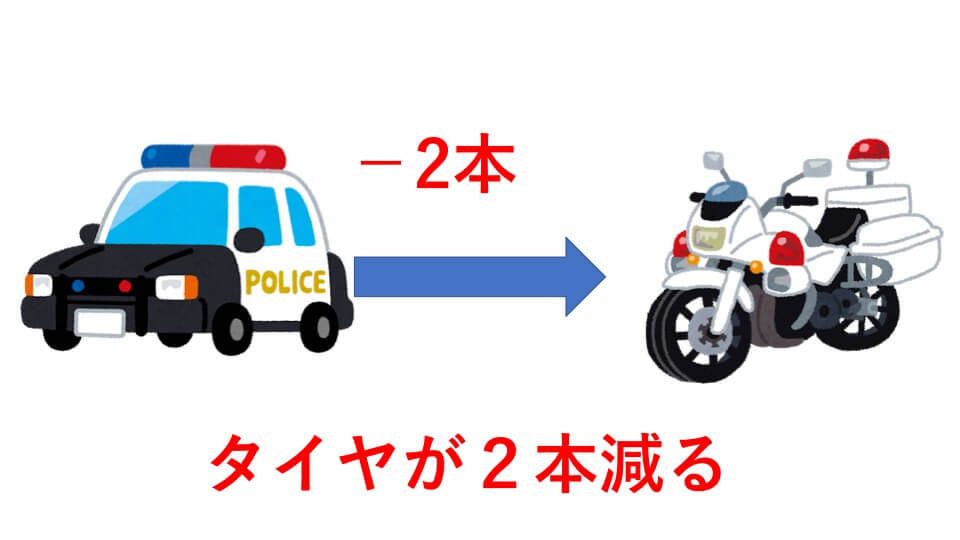
上の図のように2本減ります。8本減らすためには
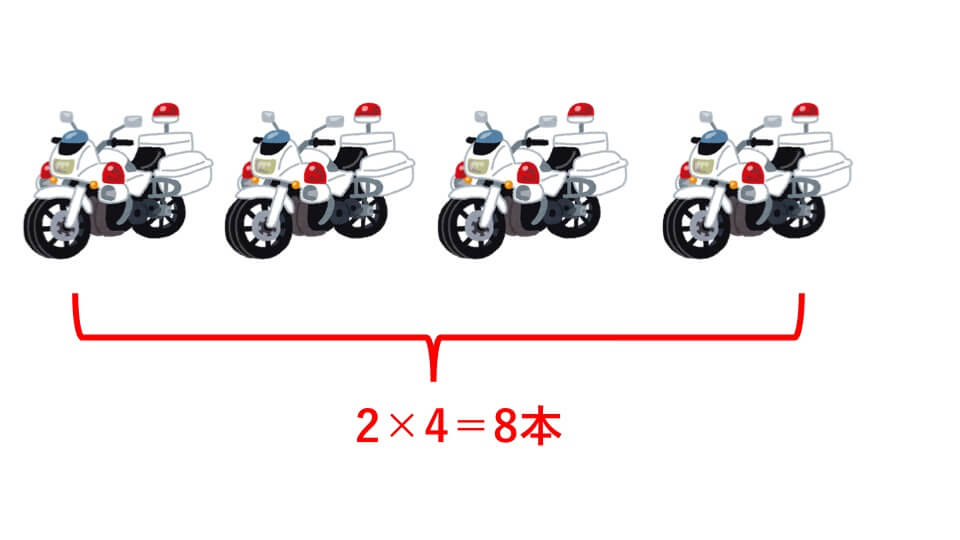
上の図のように4台を白バイに変えればいいです。
そしてパトカーの数は
7-4=3(台)
よって答えパトカー3台 白バイ4台
つるかめ算③面積図を用いた問題
例題3
太郎くんの家から、学校まで2000mあります。太郎くんは分速50mの速さで歩き、分速150mの速さで走ります。太郎くんが家から学校まで24分でいくには、何分走ればいいですか?
解説
24分間全て歩いたと考えて解く方法と、24分間全て走ったと考えて解く方法の2つの方法が考えられます。どちらの考え方も、実際の距離との間に差ができることから、この差を2つの速さの差で割ると、それぞれのかかった時間を求めることができます。
これを面積図を使って表すと下の図のようになります。
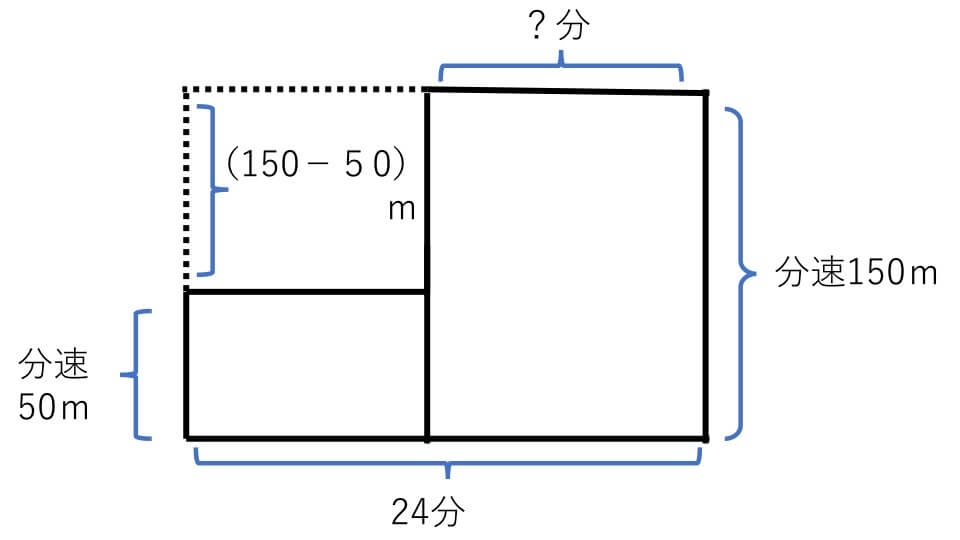
24分間全て走ったと考えると距離は
150×24=3600(m)
実際との距離の差は
3600-2000=1600(m)
この差を2つの速さの差で割ると、それぞれのかかった時間を求めることができるので、式は
1600÷(150-50)=16(分) これは歩いた時間です。
よって走った時間は
24-16=8(分)
答え 8分走った
別解
24分間全て歩いた考えると距離は
50×24=1200(m)
実際との距離の差は
2000-1200=800(m)
この差を2つの速さの差で割ると、それぞれのかかった時間を求めることができるので、式は
800÷(150-50)=8(分)
答え8分走った
つるかめ算④ 仮定をして考える問題
例題4
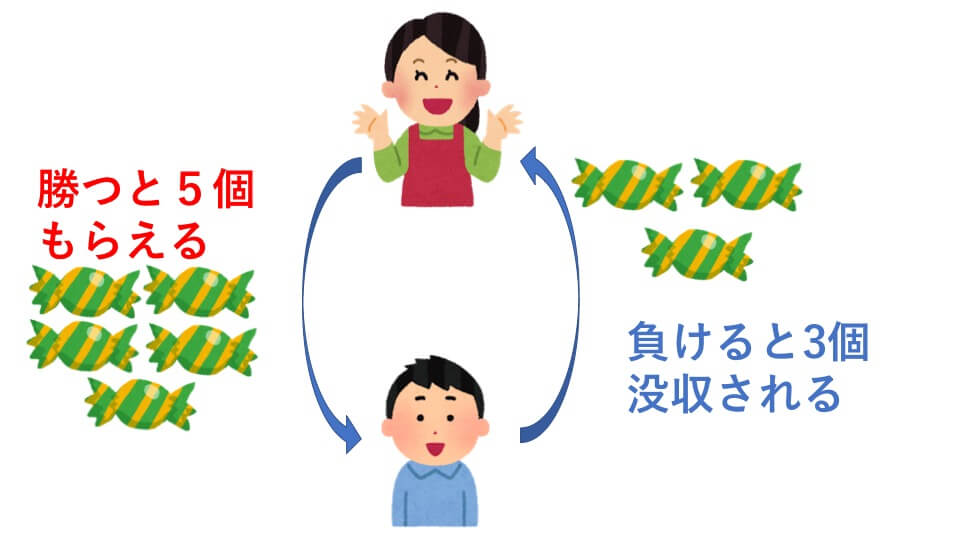
太郎くんはあるゲームをお母さんとしました。ゲームに勝つと5個飴玉が貰えます。しかし負けると3個飴玉を没収されます。太郎くんはこのゲームを合計20回行いました。最終的に太郎くんは飴玉を12 個手に入れることができました。太郎くんは何回このゲームに勝ちましたか?
解説
全てゲームに勝ったと仮定したときの飴玉の個数と実際に貰った飴玉の個数との差をまず考えます。
全てゲームに勝ったときの飴玉の個数は
5×20=100(個)
実際に貰った飴玉の個数との差は
100-12=88(個)
次にゲームに勝ったときと負けたときの飴玉の個数の差を求めます。
勝ったときと負けたときの飴玉の個数の差は
5+3=8(個)
よって負けた回数は
88÷8=11(回)となるので勝った回数は
20-11=9(回)
答え9回勝った
つるかめ算⑤ 表を用いて考える問題
例題5
太郎くんは1個10円、20円、30円する3種類の飴玉を合わせて10個買いました。飴玉を買った個数は30円が一番多く、その次は20円、10円の順に多く買いました。このときの値段は230円でした。飴玉はそれぞれ何個買いましたか?
解説
条件が3つ以上ある場合は、表を書いて、答えを求めていきます。買った個数が多い順に調べていくと下の表のようになります。
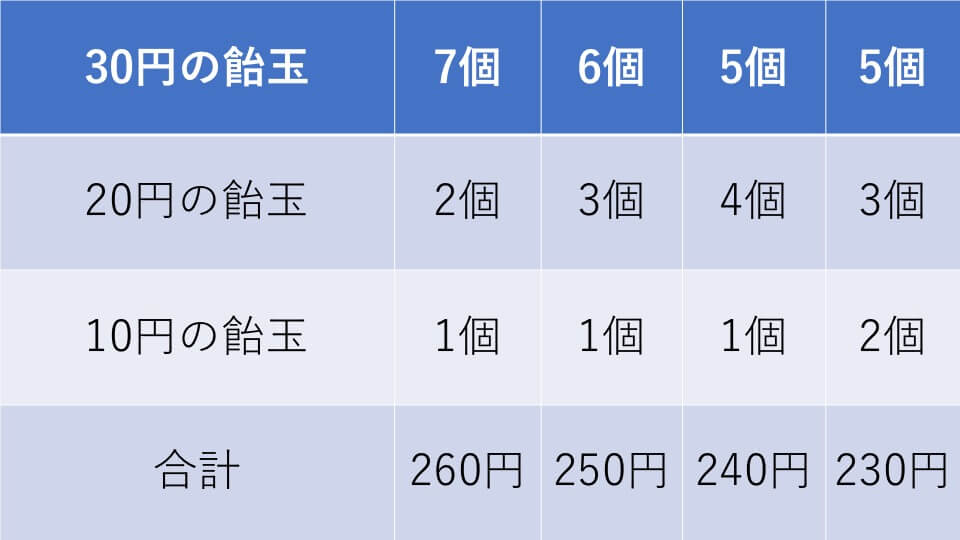
よって答え30円を5個、20円を3個、10円を2個
まとめ
いかがだったでしょうか?
つるかめ算は難しい問題です。今回の問題でも一発で解けた人は少ないのではないでしょうか。同じ問題でいいので今回学習した例題5つを繰り返し解いて理解を深めていってください。
この5つの問題が他の人に説明できるぐらいになったら、お手持ちの問題集で問題数をこなしていってください。
中学受験は算数や国語ではなく、「社会」の出来で合否が決まります!
そのため、第一志望に合格したいのであれば、社会を家庭学習でまず最初に固めるのが断トツの近道です!
【社会を最初に固めるべき理由】
● 算数の1点と社会の1点は、総合点で考えれば同じ1点
● 社会は暗記教科で学習センスがいらない!
● 社会は塾任せでは絶対に伸びない、家庭学習で伸ばす!
【短期間で社会の偏差値を上げたい方必見!】
短期間で偏差値を10以上アップさせた受験生多数!社会の偏差値を最速でアップできる社会に特化したスーパー教材を下記のページでご紹介しています!
\ 30日で社会の偏差値がアップ! /
スタディアップの教材はこちら
【たった5分で丸わかり】
次は植木算のポイント解説です。


