中学受験の算数で出題される単元「植木算」。等間隔で木を植えた時の木の本数と間の数、そして全体の距離と間の距離を求めます。
つるかめ算と同様に、植木算は中学受験で出題されますが、学校では教えてもらわない単元です。中学受験特有の考え方で、中学受験を経験していない人は初めて聞いた単元なのではないでしょうか。
植木算を習っていなくても、問題として出題されたとき考えれば解くことはできますが、事前に学習し、知っておくことで、その問題を楽に解けるのはもちろんのこと、見たことのある問題が出題されると精神的にも落ち着きます。
この記事では、算数が苦手な人や植木算を初めて学習する人に向けて、植木算について解説していきます。この記事を読むことで、植木算とは何か理解でき、植木算のパターンがわかるようになるでしょう。
中学受験は算数や国語ではなく、「社会」の出来で合否が決まります!
そのため、第一志望に合格したいのであれば、社会を家庭学習でまず最初に固めるのが断トツの近道です!
【社会を最初に固めるべき理由】
● 算数の1点と社会の1点は、総合点で考えれば同じ1点
● 社会は暗記教科で学習センスがいらない!
● 社会は塾任せでは絶対に伸びない、家庭学習で伸ばす!
【短期間で社会の偏差値を上げたい方必見!】
短期間で偏差値を10以上アップさせた受験生多数!社会の偏差値を最速でアップできる社会に特化したスーパー教材を下記のページでご紹介しています!
\ 30日で社会の偏差値がアップ! /
スタディアップの教材はこちら
【たった5分で丸わかり】
植木算① 3つのパターンの公式
植木算は以下のパターンに分けられ、それぞれに公式があります。
- 両端を含むパターン
- 両端を含まないパターン
- 周囲がつながっているパターン
両端を含むパターン
直線に木を植えて、その両端の場所にも木を植える
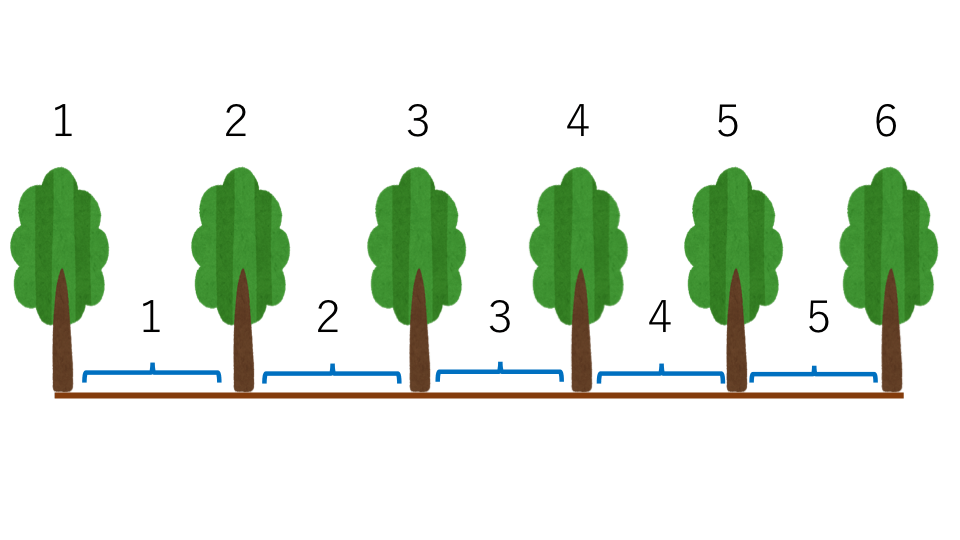
このように木を植えた場合は
木などの数=間の数+1
という公式が成り立ちます。
両端を含まないパターン
直線に木を植えますが、その両端の場所に木を植えない
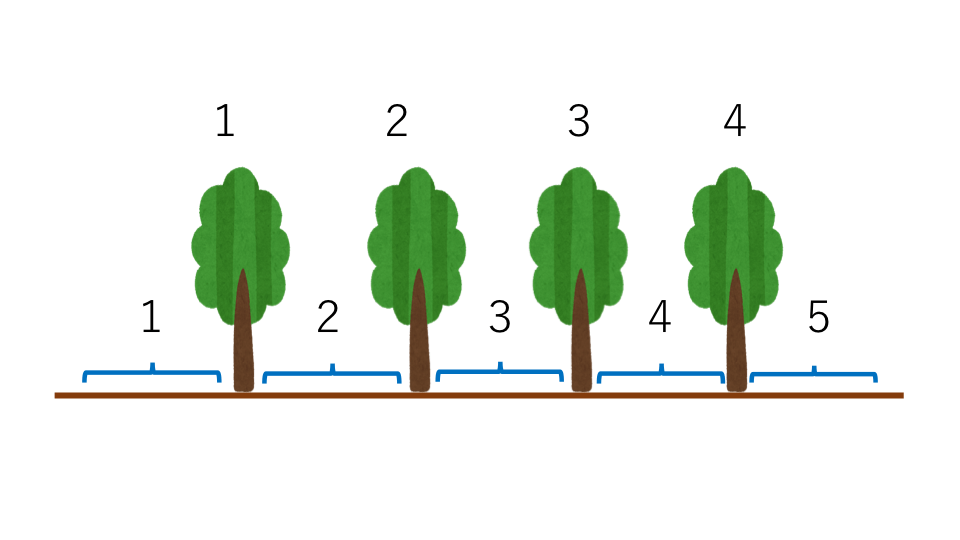
このように木を植えた場合は
木などの数=間の数−1
という公式が成り立ちます。
周囲がつながっているパターン
円状など周囲が繋がっていて木が植えられている
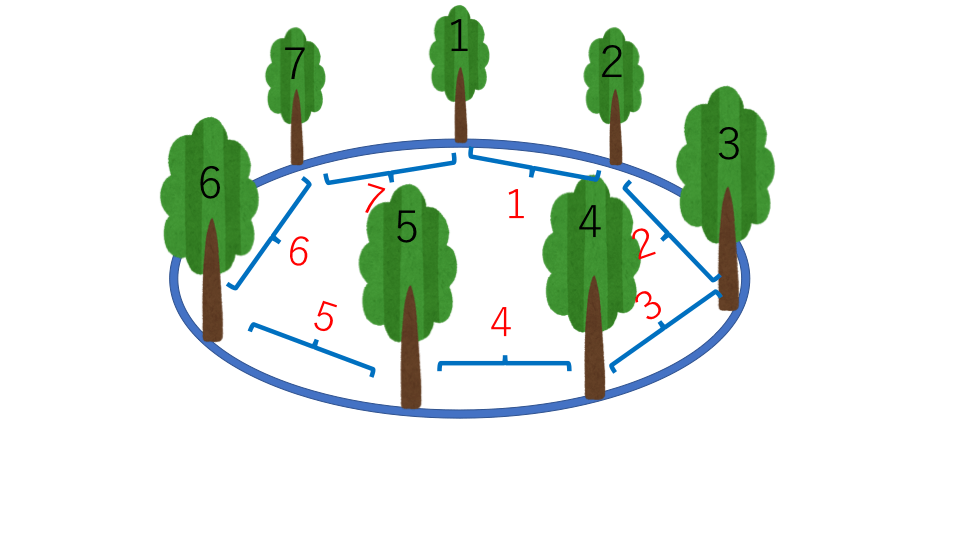
このように木を植えた場合は
木などの数=間の数
という公式が成り立ちます。
① 両端を含むパターン・・・木などの数=間の数+1
②両端を含まないパターン・・・木などの数=間の数−1
③周囲がつながっているパターン・・・木などの数=間の数
実際に例題を使って解説していきます。
植木算② 両端を含むパターン
例題1
長さ400mの真っ直ぐな道に、10mおきに木を端から端まで植えると、木は何本必要になるか求めなさい
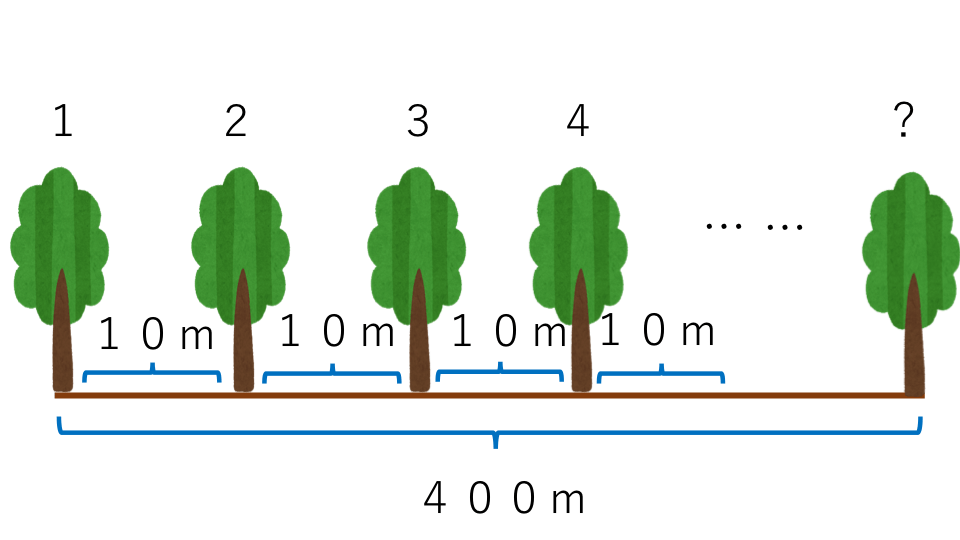
解説
まずは間の数を求めて、間の数と木の数との関係から木の数を求めていきます。
間の数は
400÷10=40(個)と求めることができます。
今回の問題は両端を含むパターンの問題なので公式、木などの数=間の数+1に当てはめて考えると、
木の数=40+1=41(本)
よって答え41本
例題2
運動会の練習のために一直線の道を200m走ることになりました。自分の走っている距離がすぐにわかるようにスタートからゴールまで20mの間隔で旗を置くことにしました。このとき必要な旗の本数を求めなさい。
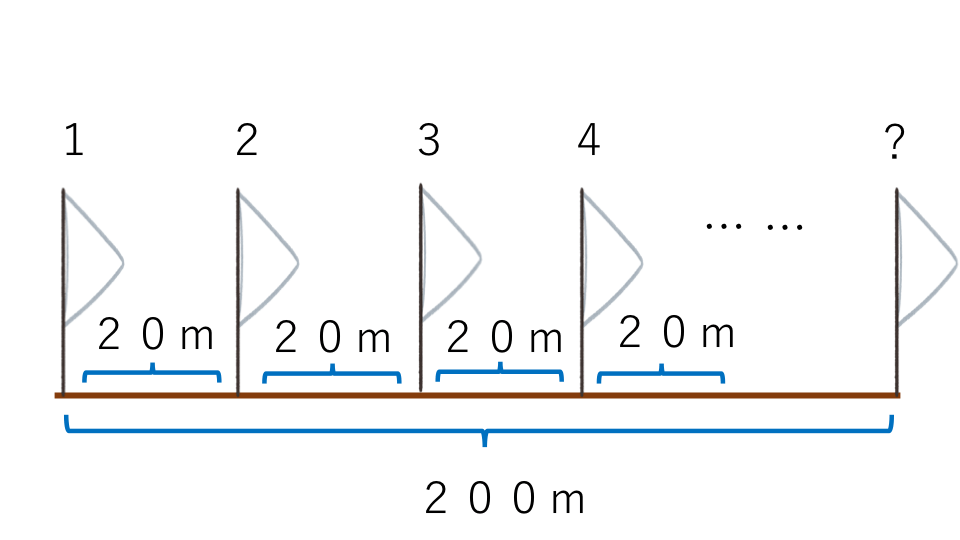
解説
植木算の問題では木以外にも問題として出題されます。木ではない問題だからといって考え方が変わるわけではありません。植木算の考え方で解いていきましょう。
まずは間の数を求めて、間の数と旗の数との関係から旗の数を求めていきます。
間の数は
200÷20=10(個)と求めることができます。
今回の問題は両端を含むパターンの問題なので公式、木などの数=間の数+1に当てはめて考えると、
旗の数=10+1=11(本)
よって答え11本
植木算③ 両端を含まないパターン
例題3
長さ240mのまっすぐな道路に20mの間隔で木を植えます。両端には木を植えないとき、木は何本必要になるか求めなさい。
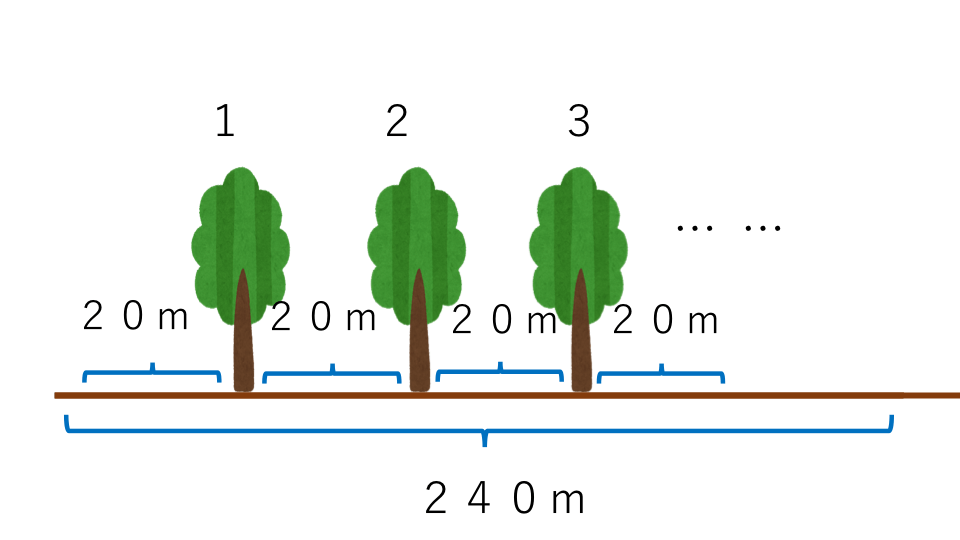
解説
まずは間の数を求めて、間の数と旗の数との関係から木の数を求めていきます。
間の数は
240÷20=12(個)と求めることができます。
今回の問題は両端を含まないパターンの問題なので公式、木などの数=間の数−1に当てはめて考えると、
木の数=12−1=11(本)
よって答え11本
例題4
132m離れた2本の電柱の間に、10本の木を同じ間隔で植えることにしました。このときの間隔は何mになりますか?
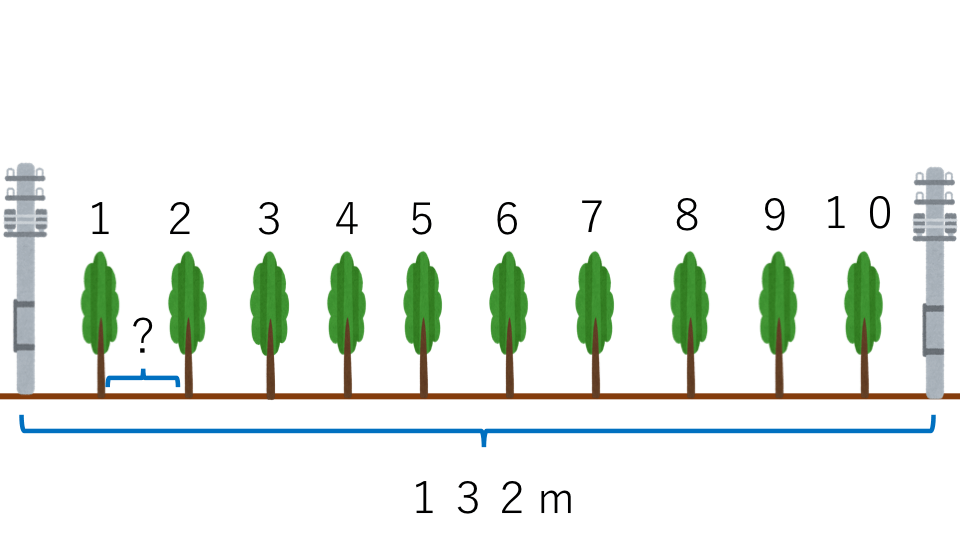
解説
今までの問題とは少し違います。今回は木の本数を求めるのではなく、間隔を求める問題です。
両端に電柱があるので両端を含まないパターンの問題として考えます。木などの数=間の数−1を間の数=木などの数+1に式を変形し、その式に当てはめて間の数を求めると、
間の数=10+1=11(個)
よって間隔は
132÷11=12(m)
答え12m
植木算④ 周囲がつながっているパターン
例題5
池の周りを1周する道に15mおきに木を植えると40本木が必要でした。このときの池の周りの道の長さは何mあるか求めなさい。
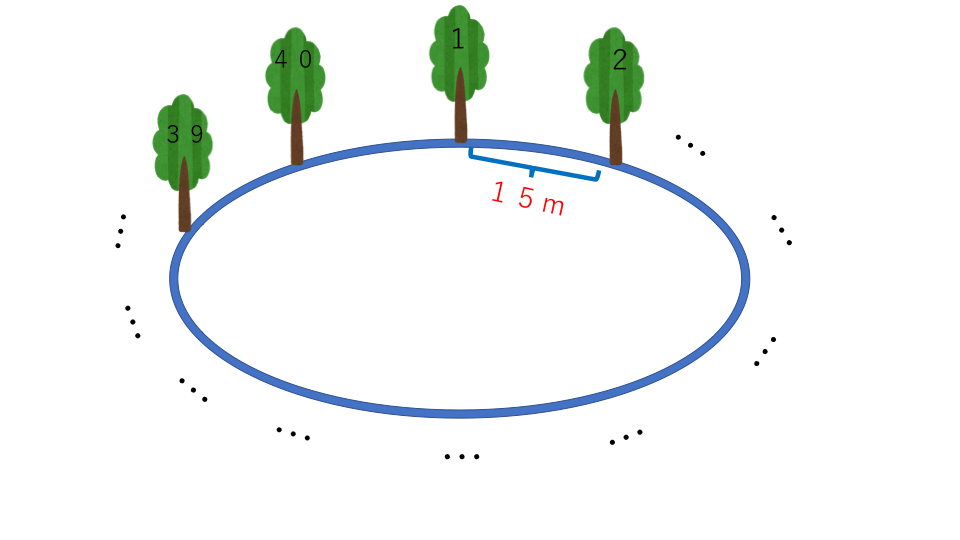
解説
池のように、周囲が繋がっている場合は、木の数と間の数との関係から間の数を求めて、周りの長さを求めていきます。
今回の問題は周囲がつながっているパターンなので公式は、木などの数=間の数となるので、間の数40個となります。
ですので周りの長さは
15×40=600(m)
よって答え600m
植木算⑤ パターン以外の問題
植木算ではパターン以外の問題も出題されます。
しかしよく考えると、どれかのパターンと似たような考え方をして解く問題がほとんどです。
実際に例題を解いて考えてみましょう。
例題6
長さ5cmのテープを10本繋いで、1本にしたいと思います。繋ぎ目は1cmずつ重ねてつけるとすると、何cmのテープができるか求めなさい。
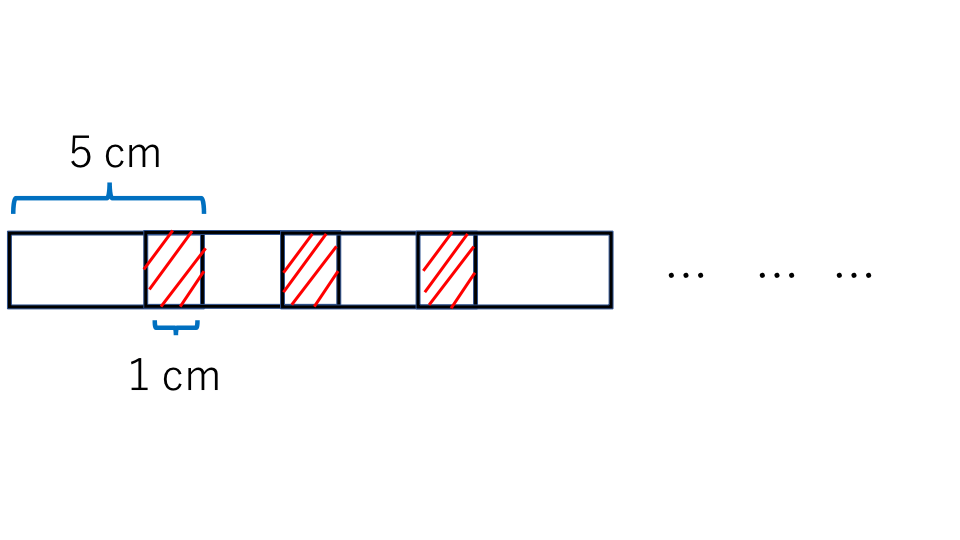
解説
繋ぎ目の数とテープの数との関係から、それぞれの長さの合計を考えます。
繋ぎ目の長さは1cmで、繋ぎ目の数は(10−1)個できるので、繋ぎ目の長さの合計は
1×(10−1)=9(cm)となります。
長さ5cmが10本あるので、テープの長さの合計は
5×10=50(cm)となります。
重ねたテープの長さはテープの長さの合計から繋ぎ目の長さの合計を引けば求めることができるので、
50−9=41(cm)
よって答え41cm
例題7
10cmのテープを10本繋ぎ合わせると、82cmになりました。繋ぎ目の部分は全て同じ長さだとすると、何cmずつ重ねましたか?
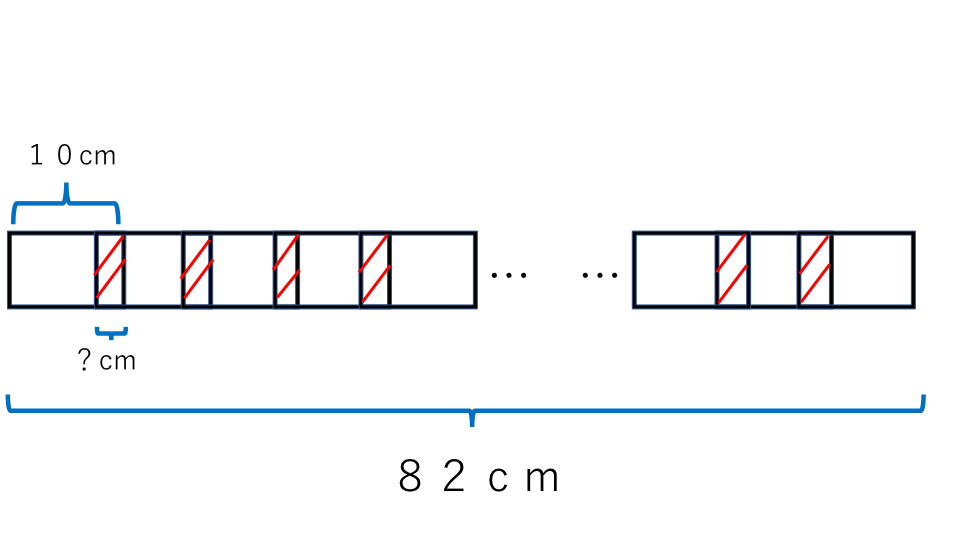
解説
例題6と同様に繋ぎ目の数とテープの数との関係から求めます。まずは繋ぎ目の数を求めます。10本のテープを繋ぎ合わせたので、繋ぎ目の数は
10−1=9(個)となります。
繋ぎ目の長さの合計は、テープの合計の長さか80cmを引けば求めることができるので、
10×10−82=18cmとなります。
繋ぎ目の長さは平等に9個に分けられるので、繋ぎ目1つ分の長さは
18÷9=2(cm)
よって答え2cm
まとめ
いかがだったでしょうか?植木算はそこまで難しくなく3つのパターンのどれかに当てはめて考えることで簡単に解けることを実感してもらえたと思います。
実際の問題では、今回のように問題文に対するイラストは書かれていないので、テストで出題されたときは簡単にイラストを書いて考えてみるとより理解しやすくなると思います。
中学受験は算数や国語ではなく、「社会」の出来で合否が決まります!
そのため、第一志望に合格したいのであれば、社会を家庭学習でまず最初に固めるのが断トツの近道です!
【社会を最初に固めるべき理由】
● 算数の1点と社会の1点は、総合点で考えれば同じ1点
● 社会は暗記教科で学習センスがいらない!
● 社会は塾任せでは絶対に伸びない、家庭学習で伸ばす!
【短期間で社会の偏差値を上げたい方必見!】
短期間で偏差値を10以上アップさせた受験生多数!社会の偏差値を最速でアップできる社会に特化したスーパー教材を下記のページでご紹介しています!
\ 30日で社会の偏差値がアップ! /
スタディアップの教材はこちら
【たった5分で丸わかり】

