中学受験の算数で出題される単元「時計算」。○時●△分時の長針と短針の角度を求める問題や長針と短針が重なる時刻を求める問題が出題されます。
「時計算」は高校受験、大学受験では出題されない中学受験特有の問題ですが、算数の基礎的な考え方を身につけるために大切な単元となります。
中学や高校で学習する文章問題や角度の問題での根本的な考えの元となります。ですので中学受験のうちに基礎を作って今後の学習に備えましょう。
この記事では時計算のやり方を詳しく解説しています。
時計算を初めて学習する人や、時計算が苦手な人、算数が苦手な人でも理解できる内容です。この記事を読むことで時計算のやり方が理解できます。
中学受験は算数や国語ではなく、「社会」の出来で合否が決まります!
そのため、第一志望に合格したいのであれば、社会を家庭学習でまず最初に固めるのが断トツの近道です!
【社会を最初に固めるべき理由】
● 算数の1点と社会の1点は、総合点で考えれば同じ1点
● 社会は暗記教科で学習センスがいらない!
● 社会は塾任せでは絶対に伸びない、家庭学習で伸ばす!
【短期間で社会の偏差値を上げたい方必見!】
短期間で偏差値を10以上アップさせた受験生多数!社会の偏差値を最速でアップできる社会に特化したスーパー教材を下記のページでご紹介しています!
\ 30日で社会の偏差値がアップ! /
スタディアップの教材はこちら
【たった5分で丸わかり】
時計算① 時計算とは?
時計は円形をしているので、当然一周は360°です。そこで一番長い針(長針)は1時間で一周し、一番短い針(短針)は12 から1、1から2のように1時間で12 等分されているうちの1等分進みます。ですので時計の長針は1時間に360°動き、短針は1時間で30°動きます。
このときの時計の長針と短針による旅人算を時計算と言います。
長針と短針の速さに関して、
長針は1分間に360°÷60=6°動き、
短針は1分間に30°÷60=0.5°動きます。
また長針は短針に1分間に6°-0.5°=5.5°近づき、遠ざかります。
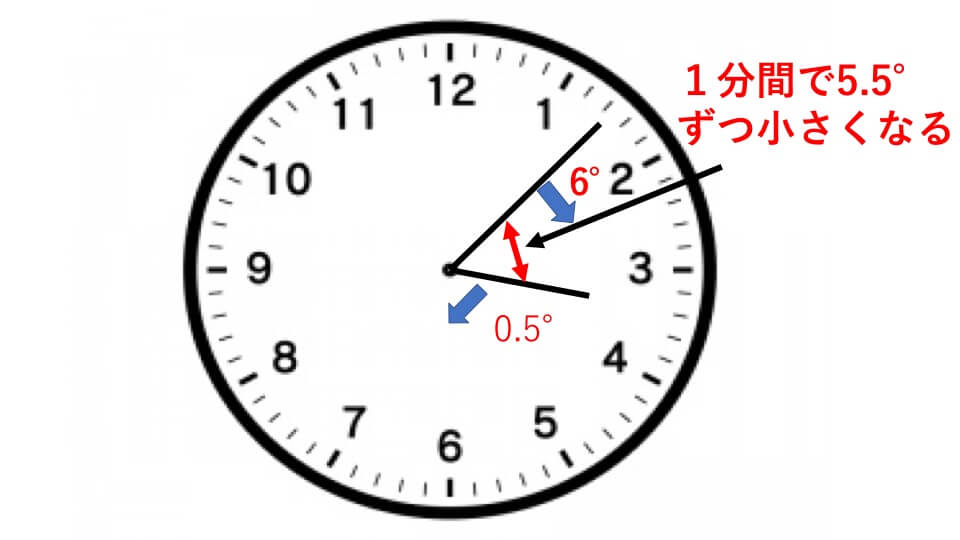
- 長針が1分間に動く角度:6°
- 短針が1分間に動く角度:0.5°
- 長針が短針1分間に近づく(遠ざかる)角度:5.5°
時計算② 角度を求める問題
例題1
下の時計を見てください。長針と短針が作る小さい方の角度は何度が求めなさい。
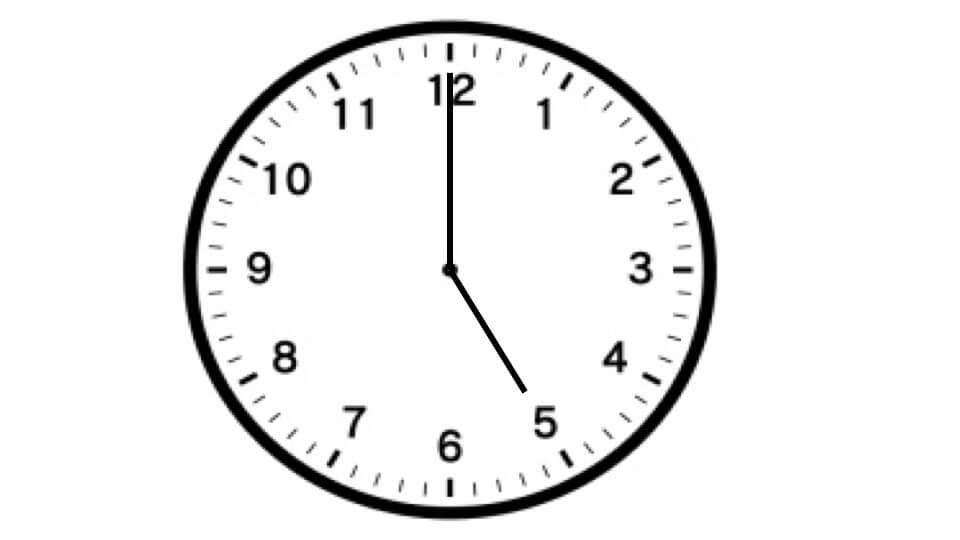
解説
時計の文字盤は1-12と目盛りで12 等分されているので、目盛りと目盛りの間の角度は
360°÷12 =30°となります。
よって問題のように5時を示すときの長針と短針が作る小さい方の角度は
30°×5=150°
答え150°
例題2
下の時計を見てください。10分後、長針と短針はそれぞれ何度動くのか求めなさい。
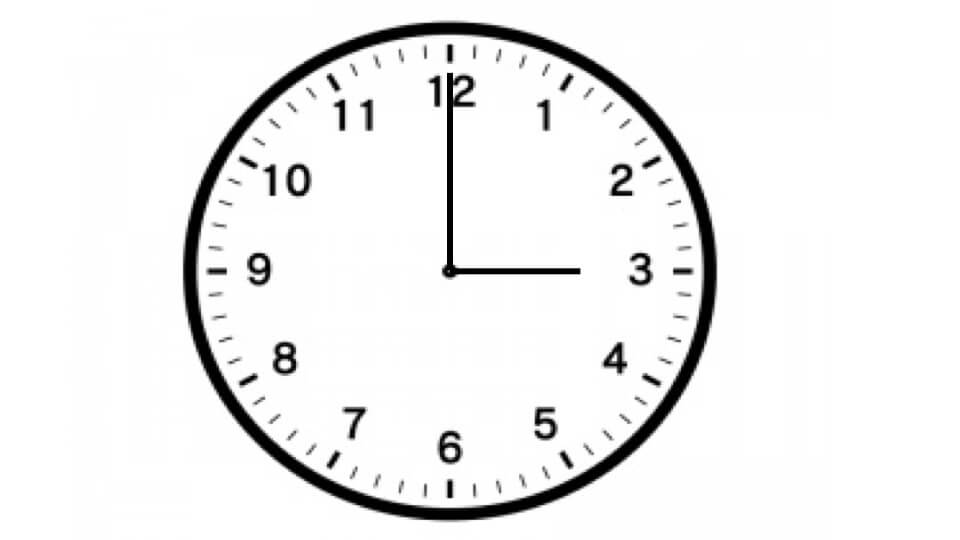
解説
長針は60分間で1周360°動くので、長針が1分間に動く角度は、
360°÷60=6°
よって、10分間に長針が動く角度は、
6°×10=60°
また短針は60分間で1目盛り30°動くので、短針が1分間に動く角度は、
30°÷60=0.5°
よって10分間に短針が動く角度は、
0.5°×10=5°
答え 長針:60° 短針:5°
例題3
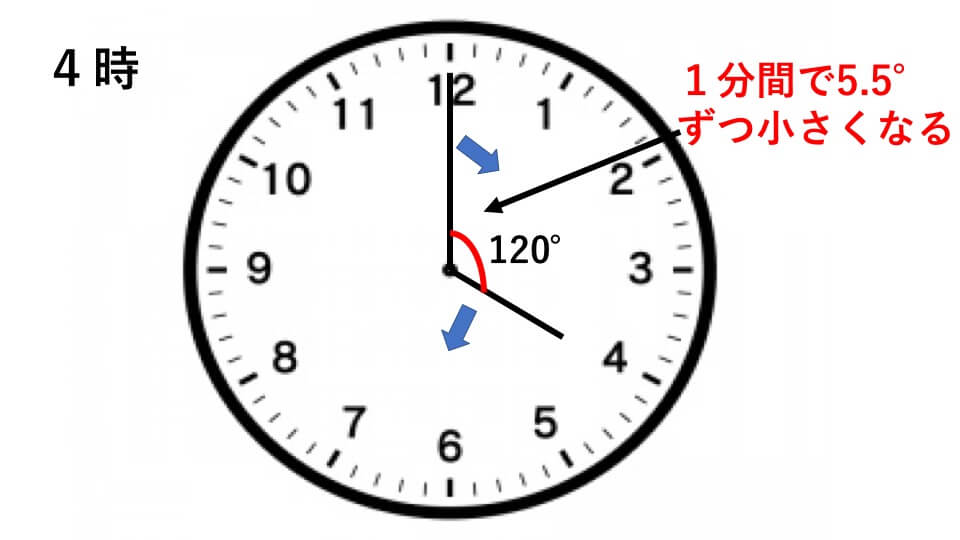
下の時計を参考にして4時20分の長針と短針が作る小さい方の角度は何度か求めなさい。
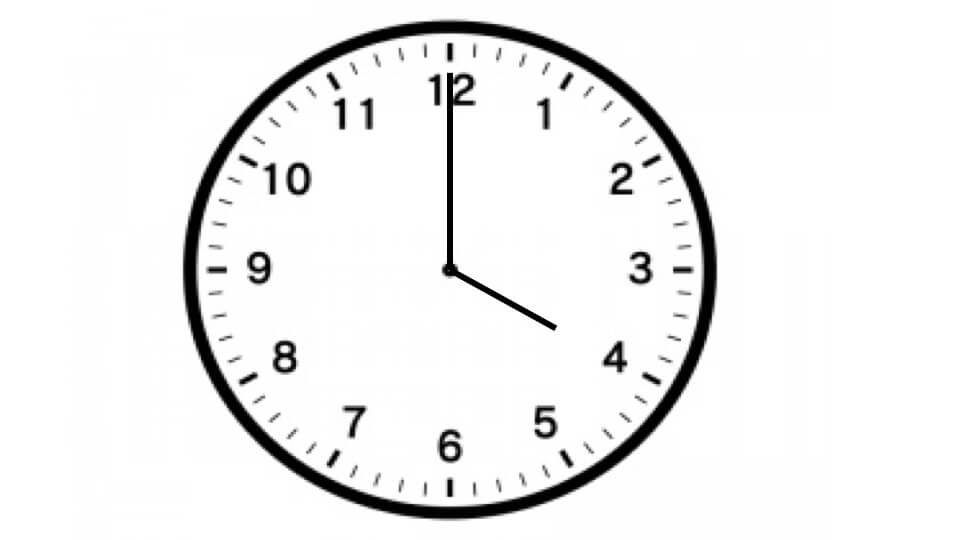
解説
時計の文字盤は1-12目盛りで12 等分されているので、目盛りと目盛りの間の角度は
360°÷12 =30°となります。
よって4時を示す時の長針と短針が作る小さい方の角度は
30°×4=120°と分かります。
長針が1分間に動く角度は6°、短針が1分間に動く角度は0.5°なので、1分間に長針は短針に
6°−0.5°=5.5°ずつ近づいていきます。
4時20分は4時から20分後の角度となるので、4時を基準として考え、そこから20分経過した角度を求めることで答えを導き出せます。
20分間では
5.5°×20=110°近づくとわかります。
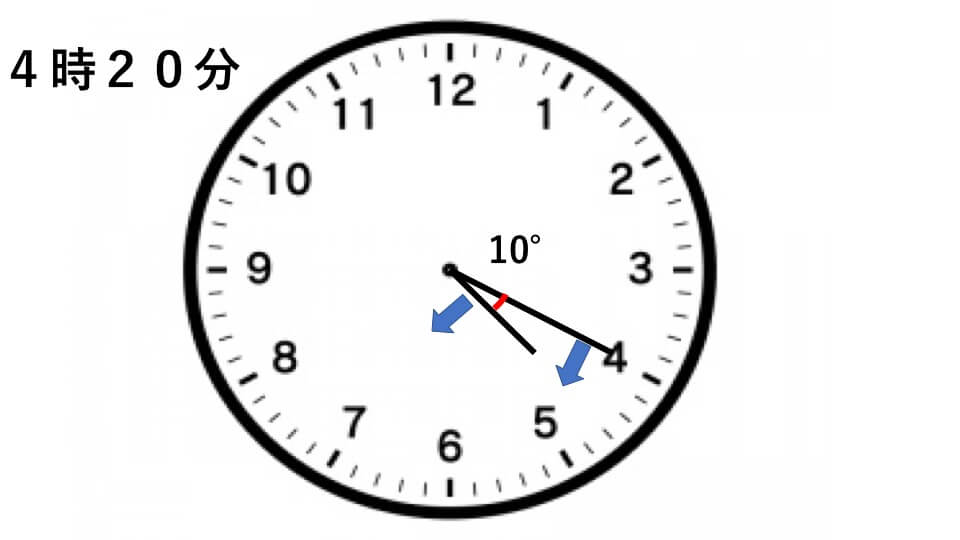
ですので4時20分の長針と短針が作る小さい方の角度は
120°-110°=10°
答え10°
時計算③ 長針と短針の関係問題
例題4
4時と5時の間で、時計の長針と短針が重なる時刻は何時何分か求めなさい。
解説
長針と短針の旅人算で解いていきます
下の図を見てください。
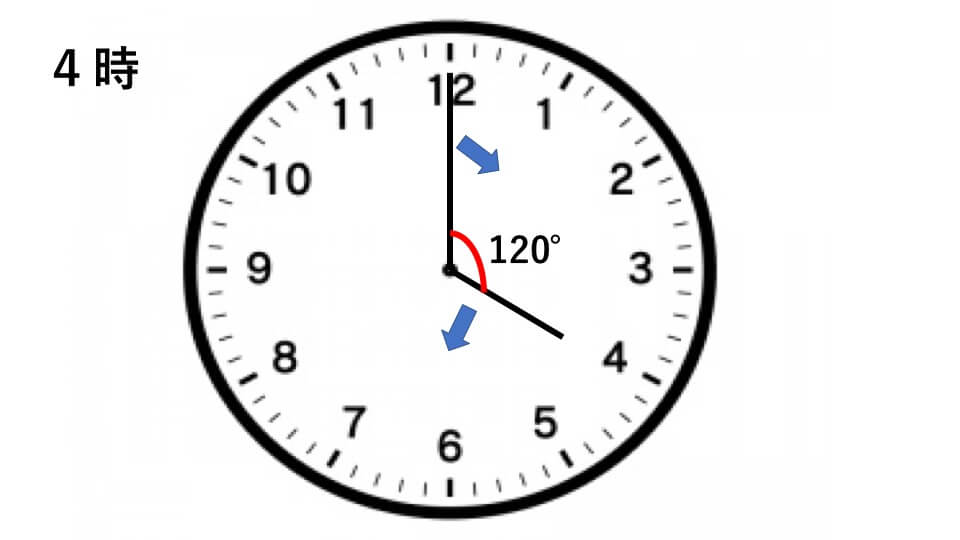
4時を示しています。4時を基準にして考えると、はじめ長針と短針の間は
30°×4=120°離れているとわかります。
長針が1分間に動く角度は6°、短針が1分間に動く角度は0.5°なので、1分間に長針は短針に
6°−0.5°=5.5°ずつ近づいていきます。
ですので、長針と短針が重なる(追いつく)のは
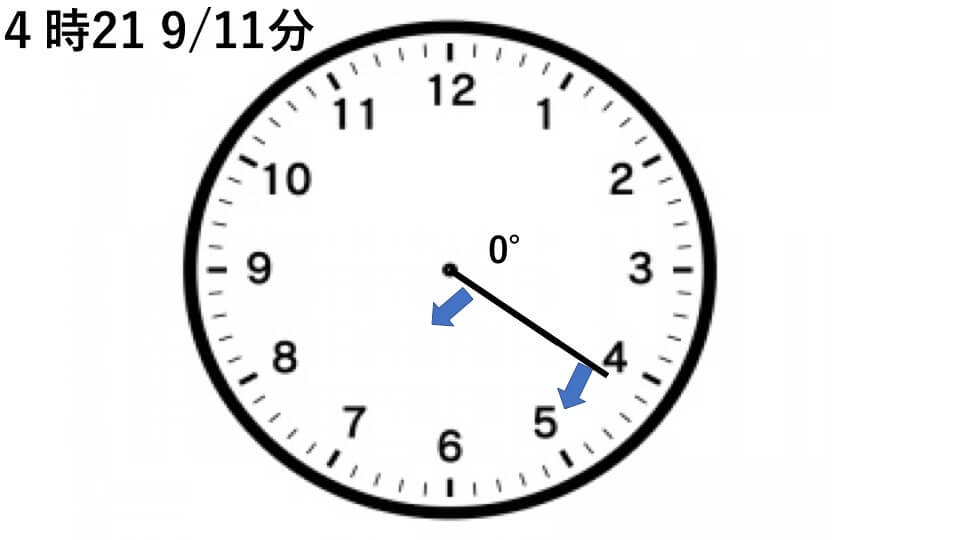
120°÷5.5°=21 9/11分後
したがって求める時刻は4時21 9/11分
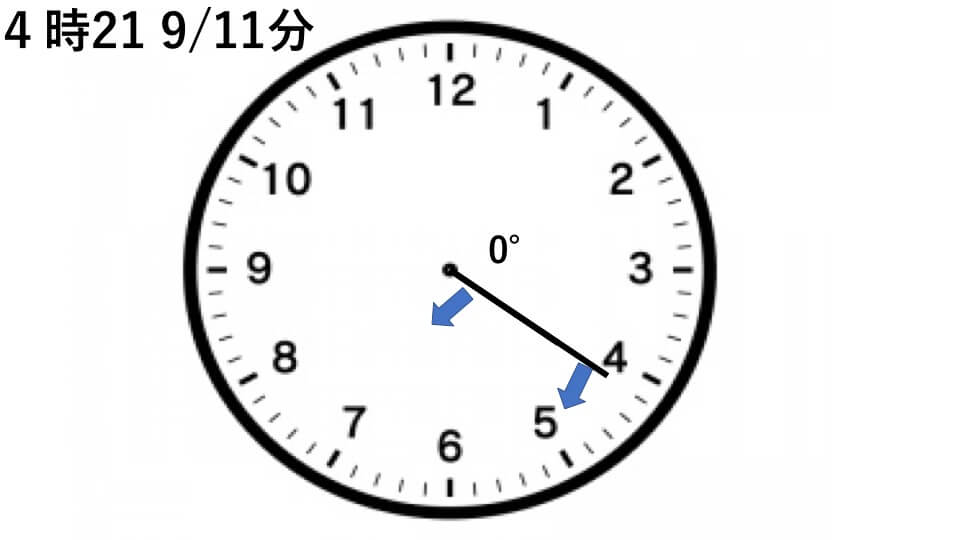
不自然な時刻だと感じる人がいるかもしれませんが、算数の問題ではよくあることなので気にしないでください。
例題5
4時と5時の間で、時計の長針と短針が反対側に一直線になるときの時刻は何時何分か求めなさい。
解説
時計の長針と短針が反対側に一直線になるときは、長針が短針より180°先に進んだときです。先程の(例題4)のときを基準にして考えます。はじめ長針と短針は重なっていて、1分間に5.5°ずつ遠ざかっていきます。
よって長針が短針より180°先に進む(長針と短針が一直線になる)のは
180°÷5.5°=32 8/11分後となります。
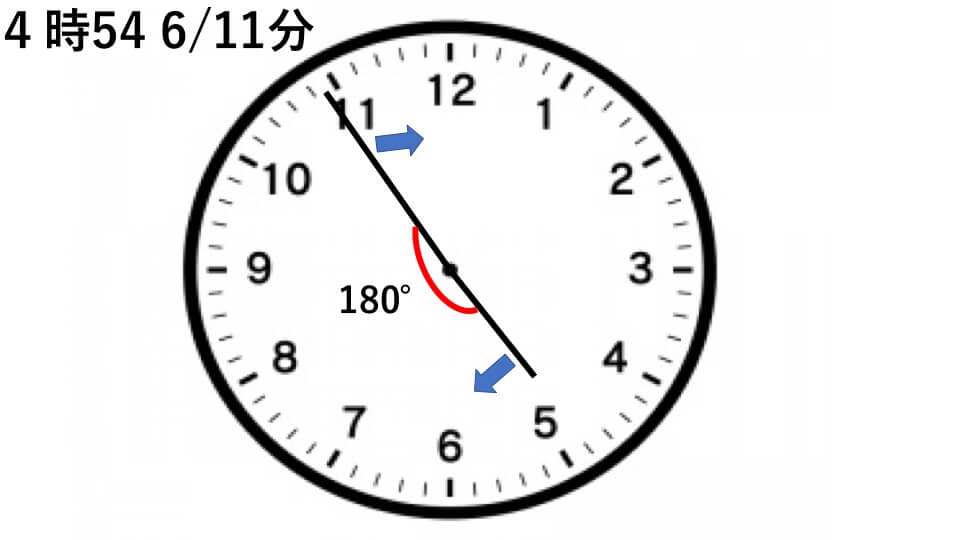
したがって求める時刻は4時21 9/11分+32 8/11分=4時54 6/11分
別解
4時を基準にして考えると、長針が短針を追いこして180°先まで進んだときに長針と短針が一直線になるので4時の地点から
120°+180°=300°動くことがわかります。長針と短針は1分間に5.5°ずつ近づいて、遠ざかっていくので、
300°÷5.5°=54 6/11分後に長針と短針が一直線になることがわかります。
よって答え4時54 6/11分
ここまでの話を公式にまとめると
重なるまでの時間=両針のつくる角度÷5.5度
①両針が重なる前
ある角度になるまでの時間=(両針のつくる角度−ある角度)÷5.5
②両針が重なった後
ある角度になるまでの時間=(両針のつくる角度+ある角度)÷5.5
例題6
4時と5時の間で、時計の長針と短針の角度が90°になるときの時刻は何時何分か求めなさい。
解説
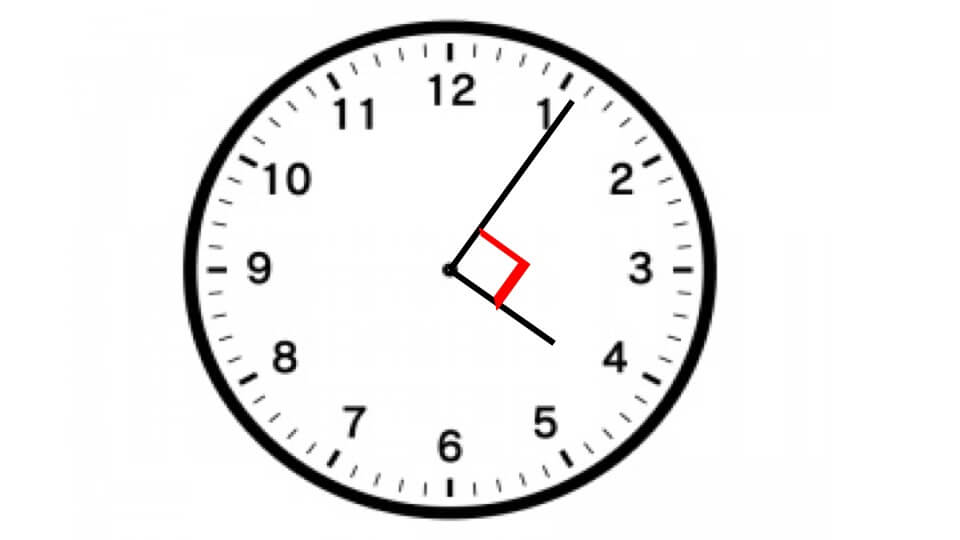
90°になるときは両針が重なる前と両針が重なった後の2パターンが考えられる
公式に当てはめて考えると
両針が重なる前
(120°−90°)÷5.5°=5 5/11分後
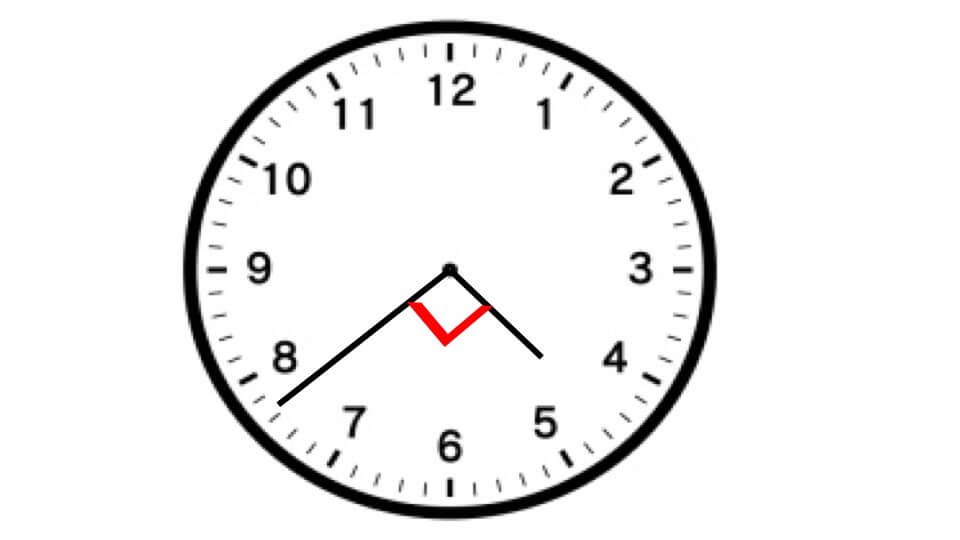
両針が重なった後
(120°+90°)÷5.5°=38 2/11分後
よって答え4時5 5/11分、4時38 2/11分
まとめ
いかがだったでしょうか?時計算はそこまで難しい問題ではなく、理解して計算をすれば簡単に解くことができます。余裕がある人は、公式を覚えて公式を使った解き方で進めていくと良いでしょう。
しかしまだ時計算に苦手意識がある人は、実際にアナログ時計を使って考えたり、普段からデジタル時計ではなく、アナログ時計を使うようにするといいと思います。
時計算は問題に慣れてさえいれば必ず解ける得点源となる分野なので、十分に復習をして自分のものにしてください。
中学受験は算数や国語ではなく、「社会」の出来で合否が決まります!
そのため、第一志望に合格したいのであれば、社会を家庭学習でまず最初に固めるのが断トツの近道です!
【社会を最初に固めるべき理由】
● 算数の1点と社会の1点は、総合点で考えれば同じ1点
● 社会は暗記教科で学習センスがいらない!
● 社会は塾任せでは絶対に伸びない、家庭学習で伸ばす!
【短期間で社会の偏差値を上げたい方必見!】
短期間で偏差値を10以上アップさせた受験生多数!社会の偏差値を最速でアップできる社会に特化したスーパー教材を下記のページでご紹介しています!
\ 30日で社会の偏差値がアップ! /
スタディアップの教材はこちら
【たった5分で丸わかり】
次は還元算のポイント解説です。


