中学受験の算数で出題される「展開図」。さまざまな問題が出題されますが、展開図のルールをしっかりとおさえることで、展開図の問題の大半が解けるようになります。また、展開図という単元は、ルールを理解することで展開図のイメージがしやすくなります。
展開図の分野をマスターすることで、今後学習することになる立体の分野や回転体の分野を理解するのが容易になってきます。逆に展開図のイメージができないまま次の単元に行ってしまうと、単純暗記で問題を解くようになってしまい、応用力が身につかなくなってしまいます。
中学受験の入試本番では、今まで出会ったことのない問題も出題されます。そこで応用力を身につけておかないと合格点を勝ち取ることはできません。そこで今回は、立方体の展開図に絞って解説していきます。
- 算数が苦手な人
- 展開図のイメージがつかない人
- そもそも展開図とは何か知らない人
そのような受験生でも理解しやすいように、わかりやすく解説しています。今回の記事を読むことで、展開図とは何か理解でき、ルールや決まりを理解する大切さが身につきます。
中学受験は算数や国語ではなく、「社会」の出来で合否が決まります!
そのため、第一志望に合格したいのであれば、社会を家庭学習でまず最初に固めるのが断トツの近道です!
【社会を最初に固めるべき理由】
● 算数の1点と社会の1点は、総合点で考えれば同じ1点
● 社会は暗記教科で学習センスがいらない!
● 社会は塾任せでは絶対に伸びない、家庭学習で伸ばす!
【短期間で社会の偏差値を上げたい方必見!】
短期間で偏差値を10以上アップさせた受験生多数!社会の偏差値を最速でアップできる社会に特化したスーパー教材を下記のページでご紹介しています!
\ 30日で社会の偏差値がアップ! /
スタディアップの教材はこちら
【たった5分で丸わかり】
そもそも展開図とは?
下の図のように、立体の表面を開いて、すべての面の1つの平面上に広げた図のことを展開図と言います。展開図は立体の組み立てがはっきりわかります。
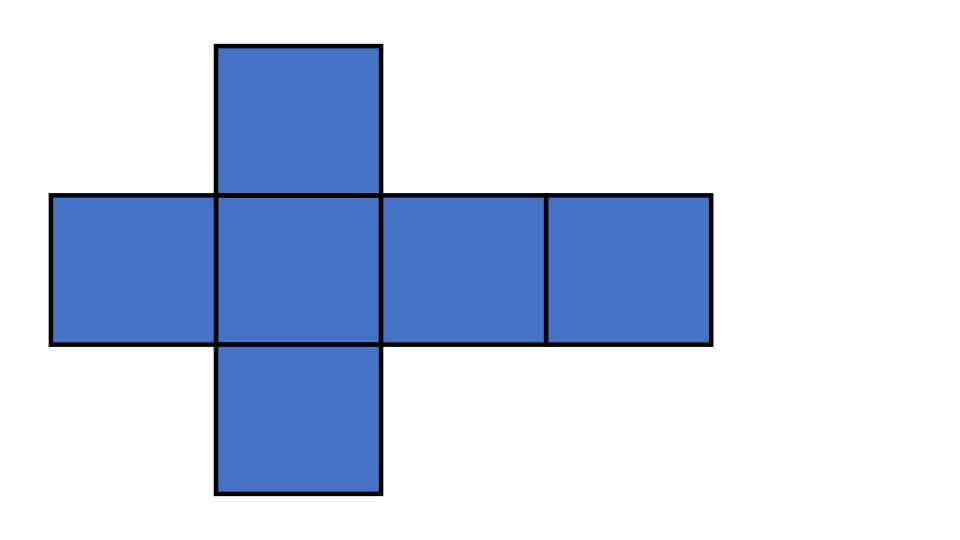
立方体の展開図は何種類ある?
立方体の展開図には下の図のように11種類あります。そして4つのパターンに分類することができます。
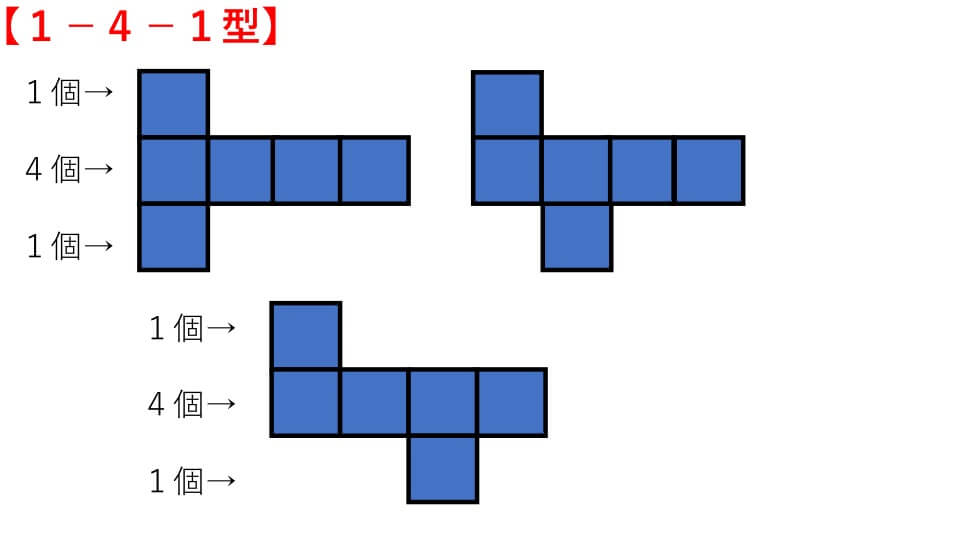
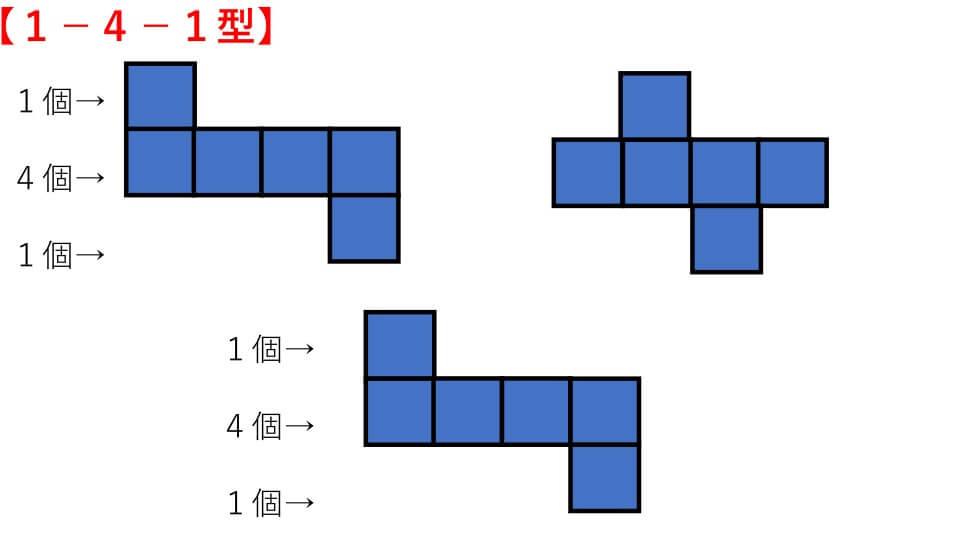
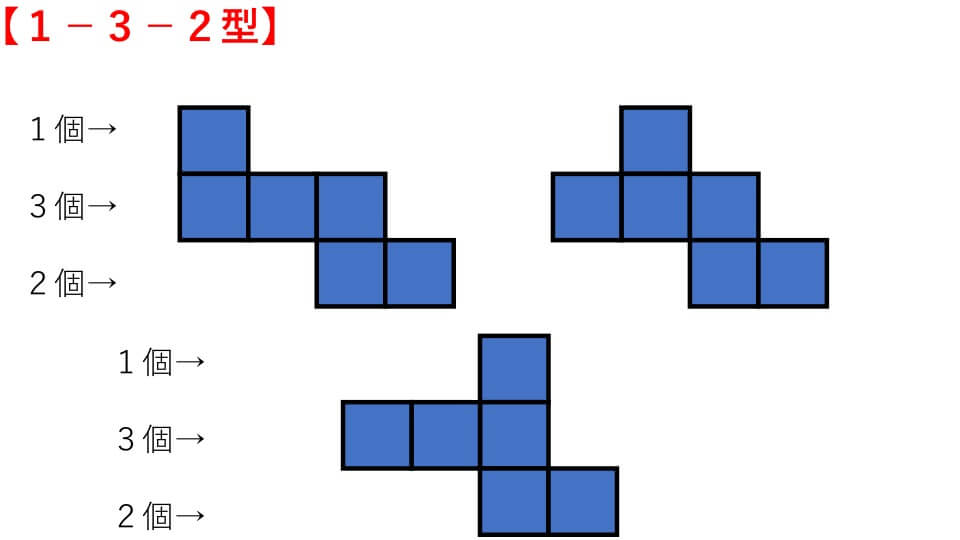
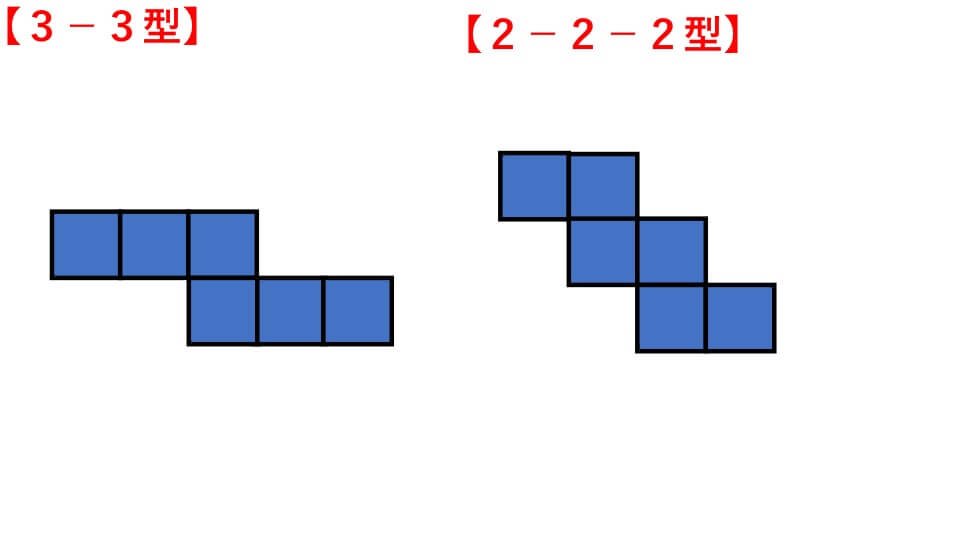
立方体の展開図は【1-4-1型】【1-3-2型】【3-3型】【2-2-2型】の4パターンに分けられます。
この4パターン以外の展開図が出てきたら、それは立方体ではありません。ですので見た目が立方体になりそうというだけで、勝手に立方体だと思い込むのはやめましょう。
時間がある人は上の展開図を自分で書いて、立方体を作ってみてください。実際に作ることで、イメージが付きやすくなります。
例題1
次の展開図を組み立てると、立方体になりますか?
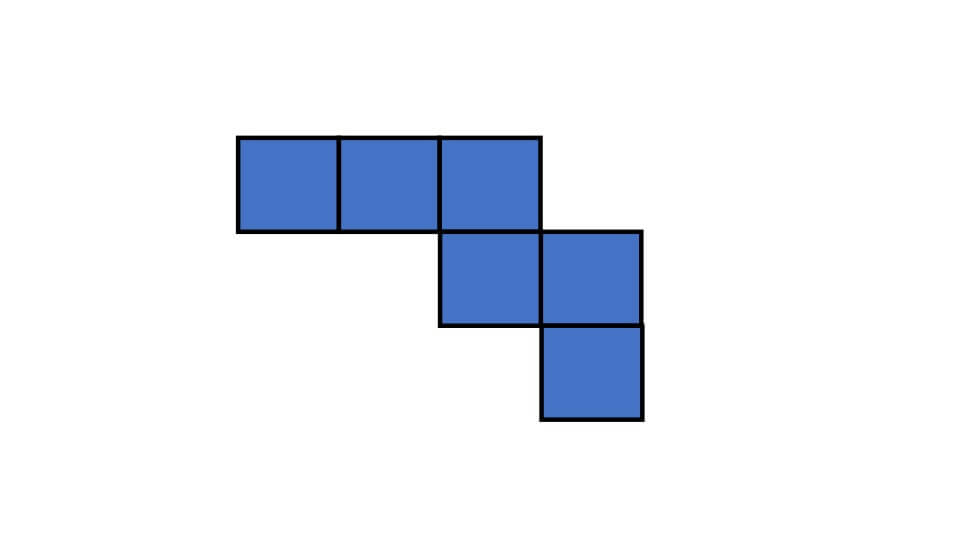
解説
下の図を見てください
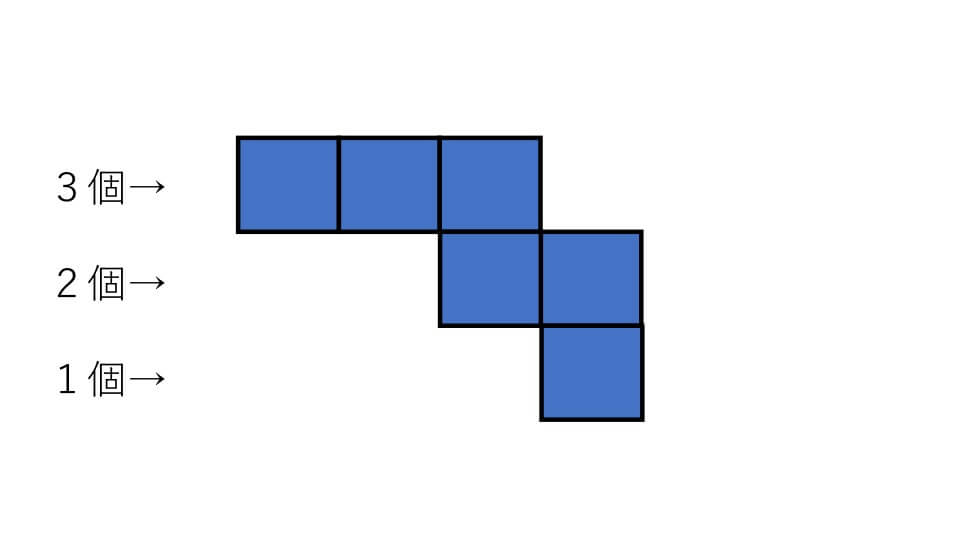
展開図は【3-2-1型】となっています。これは先ほど説明した4パターンに当てはまっていません。ですので(例題1)の展開図を組み立てても立方体にならないことがわかります。
実際に書いてみたり、頭の中で組み立てて立方体をイメージする方法はありますが、パターンを覚えて考える方が素早く正確に判断できます。
例題2
下の図をみてください。(例)の図のAの右に1つ正方形を付け加えると、正しい展開図になることを示しています。(組み立てると立方体になる展開図)
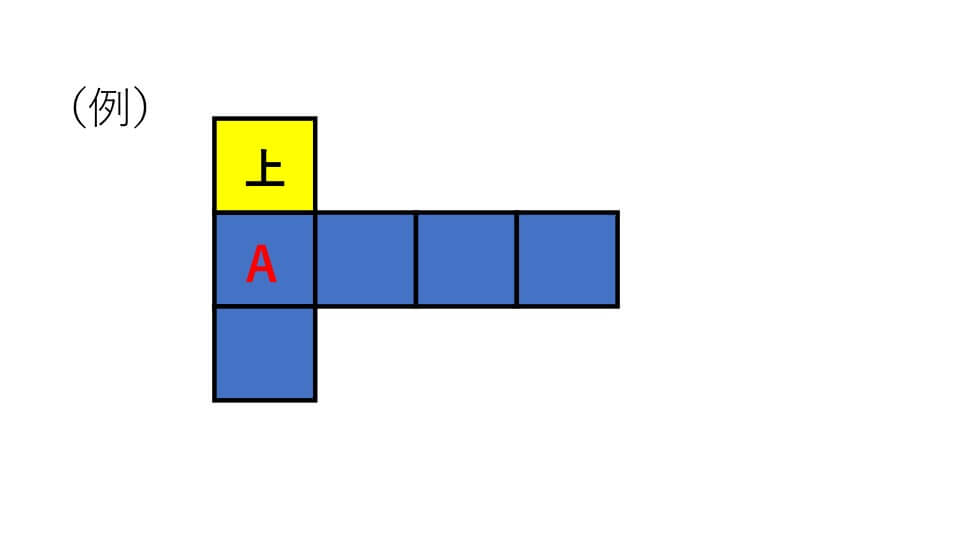
次の①②③④の図でAの正方形の上、下、右、左のどこに正方形を付け加えると、正しい展開図になりますか?
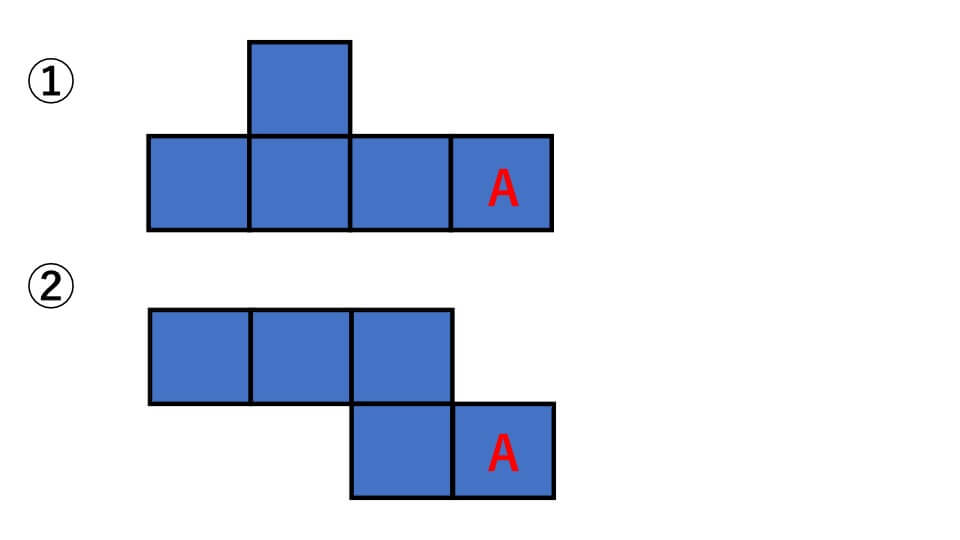
解説
立方体の展開図の4パターンを思い出してください。①-④までの展開図はすべて不十分だと分かると思います。これらの展開図を4パターンのどれかに当てはめるように考えていきます。
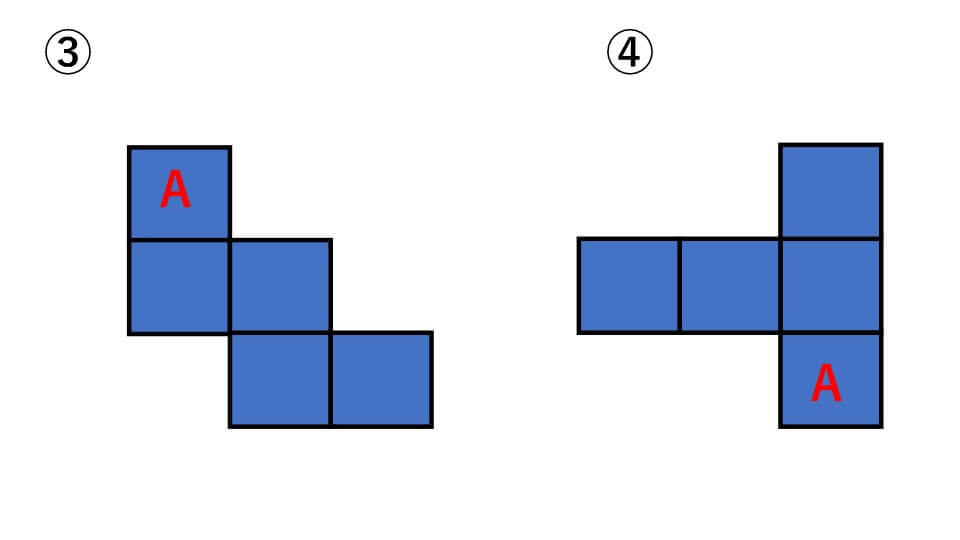
①は上から正方形が「1-4」と続いています。ですので「1-4-1」となるようにすれば正しい展開図になることがわかります。
よって答え下
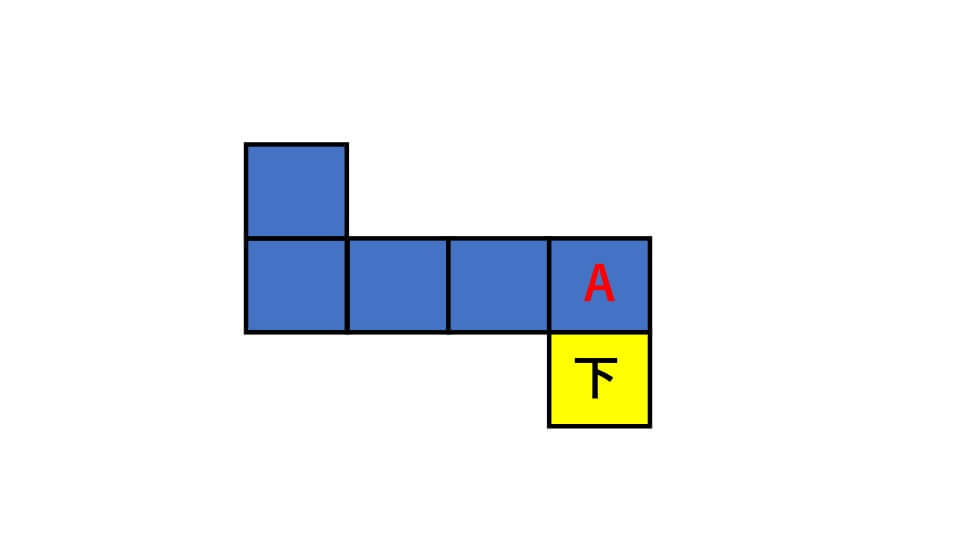
②は上から正方形が「3-2」と続いています。ですので「3-3」となるようにすれば正しい展開図になることがわかります。
よって答え右
③は上から正方形が「1-2-2」と続いています。ですので「2-2-2」となるようにすれば正しい展開図になることがわかります。
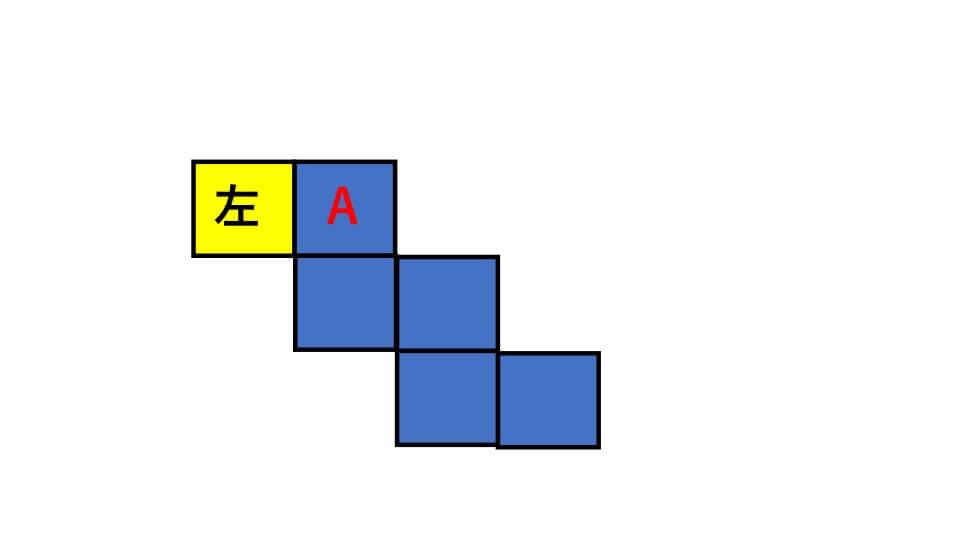
よって答え左
④は上から正方形が「1-3-1」と続いています。ですので「1-3-2」となるようにすれば正しい展開図になることがわかります。
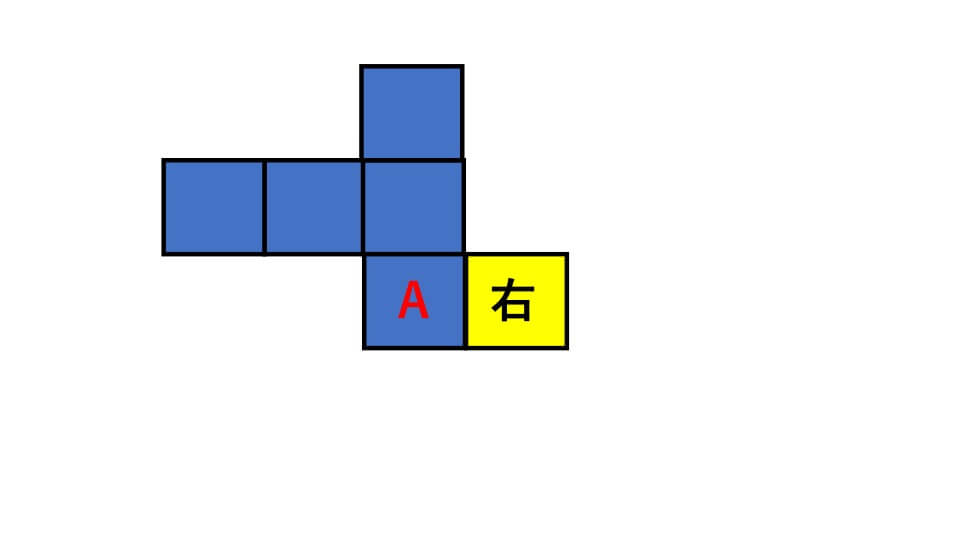
よって答え右
このように4パターンを覚えていれば立方体の展開図の問題は簡単に解くことができます。
点と点が重なる問題
まずは下の図を見てください
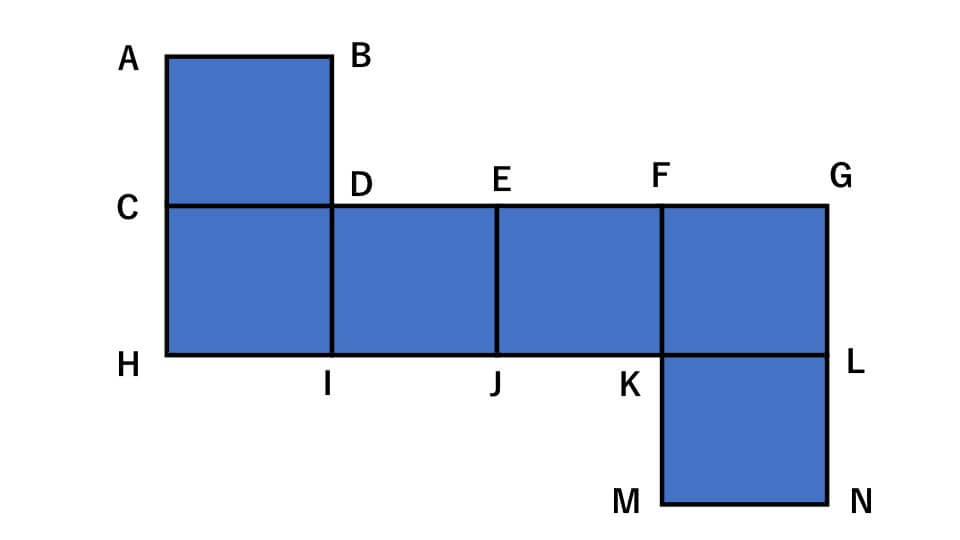
ここで頂点Nと重なる点はどの点かすぐに答えることができますか?この問題を解く時に頭の中で立方体を描いてイメージしたり、紙に直接描いたりして問題を解く人は損をしています。実はあることを知っていれば一瞬で解くことができます。「立方体の最も遠い2点は展開図では長方形の対角線の位置になる」ということを覚えてください。
いまいちわからないと思うので噛み砕いて説明していきます。
例えば、下の図のような立方体の見取り図を考えます。
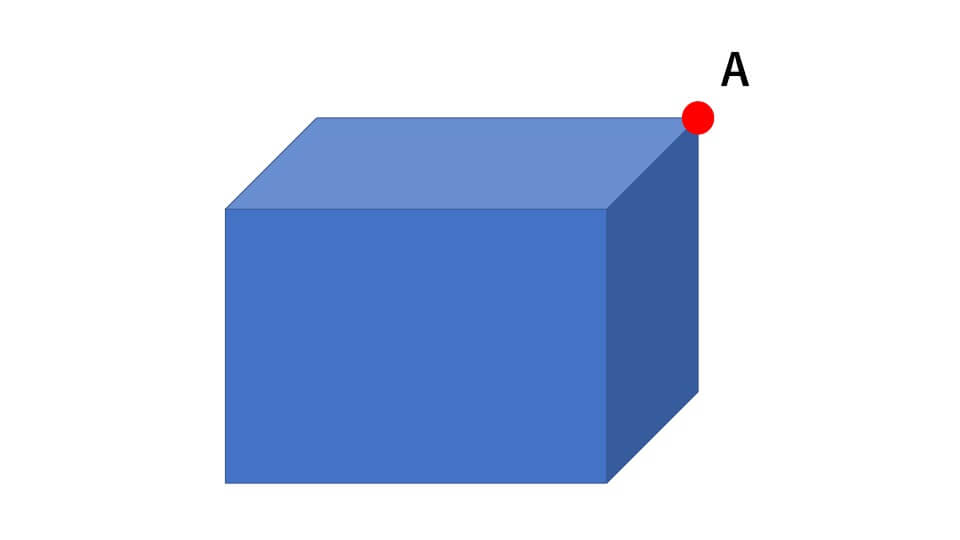
立方体の頂点は全部で8個あります。そこで今回はそのうちの一つに注目します。注目した頂点をAとします。この頂点Aから最も遠い点は青丸で示している頂点Bとわかると思います。(赤い点線は立方体を通る直線を示しています。)
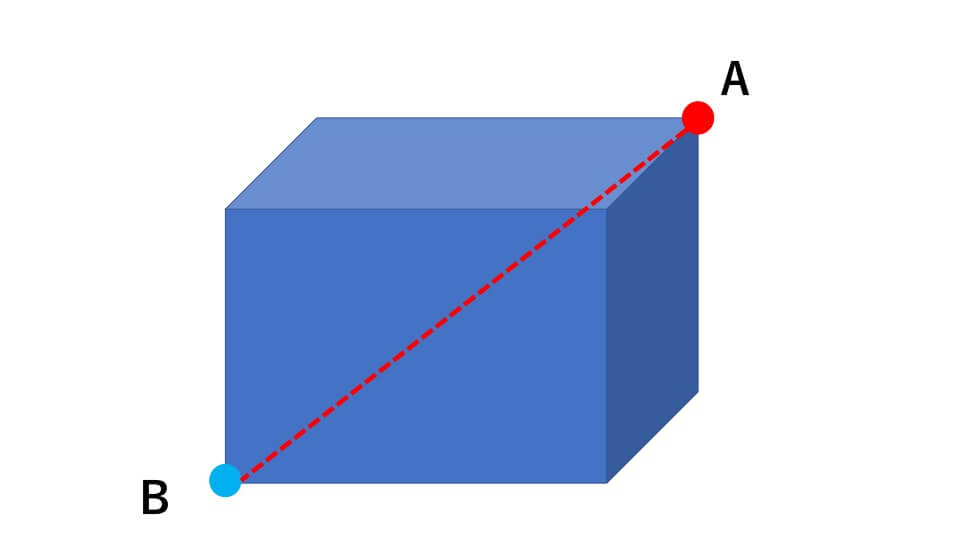
この立体の上の面を手前に広げた展開図が下の図のようになります。
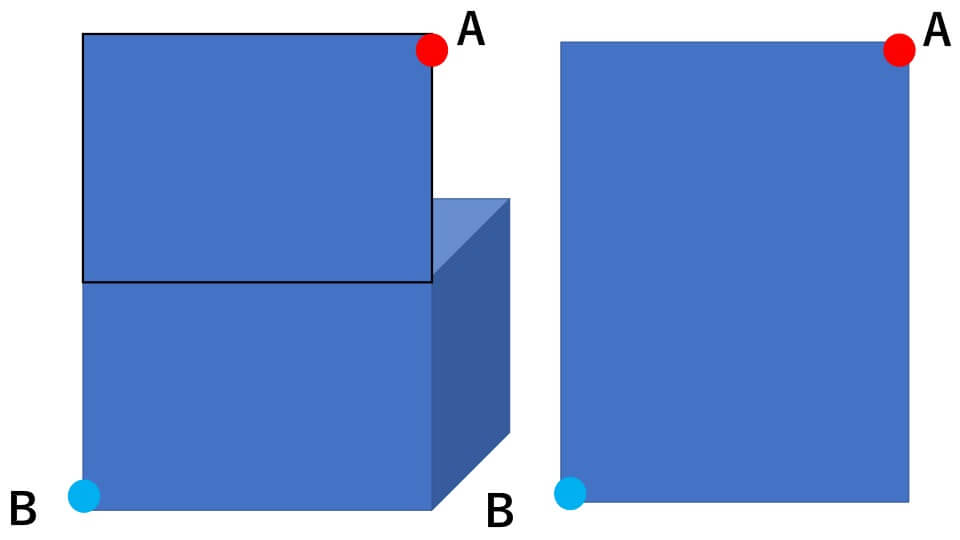
このように広げた部分の面に注目すると「立方体の最も遠い2点は、展開図上で長方形の対角線の位置になる」ことがわかると思います。
この性質を使って問題を解いて見ましょう
例題3
下の展開図で点線Nと重なる点はどの点か答えなさい。
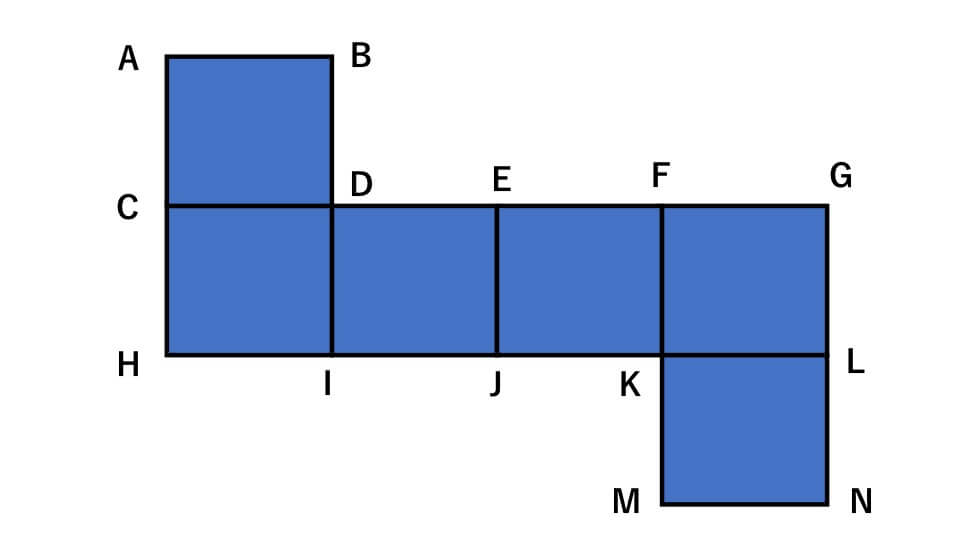
解説
点Nと重なる点を知りたいのでまずは点Nから最も遠い点はがどこにあるのか考えます。先程の「立方体の最も遠い2点は、展開図上で長方形の対角線の位置になる」という性質を使うと下の図のように点Fが点Nから最も遠い点だとわかります。
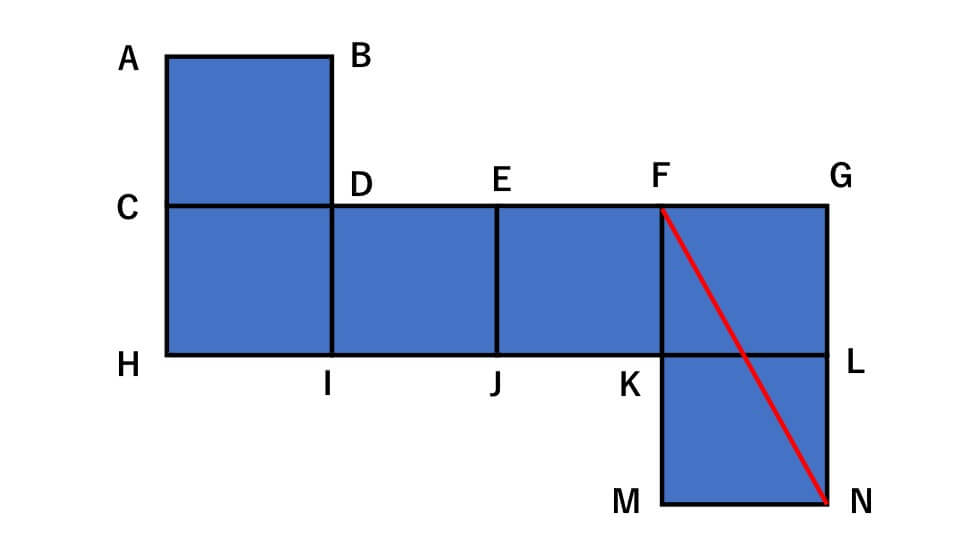
さらにここから点Fから最も遠い点がどこにあるのか考えます。そうすると下の図のように点Iが点Fから最も遠い点であることがわかります。
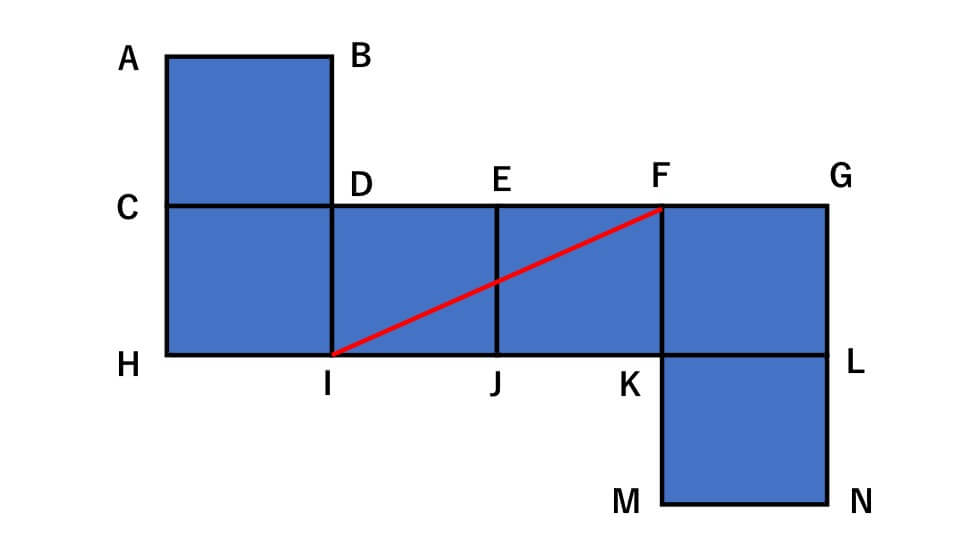
ここまでの話をまとめると
- 点Nから最も遠い点はF
- 点Fから最も遠い点はI
とわかりました。すでに気付いている人もいると思いますが、点Nと点Iはどちらも『点Fから最も遠い点』であるため全く同じ点です。
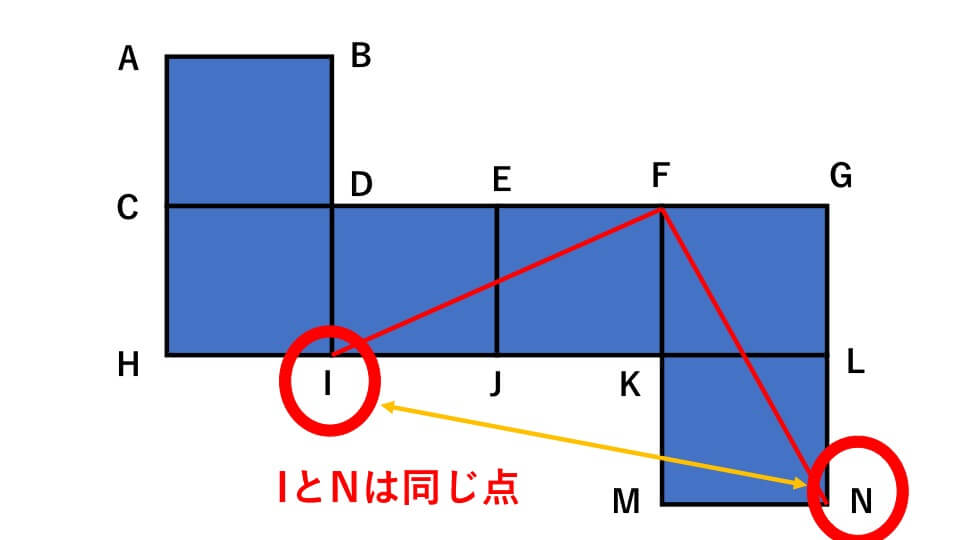
つまり、この展開図を組み立てたときに重なる点が分かります。よって答え点Iとなります。
まとめ
展開図のルールや決まりをしっかりと理解することで、簡単に問題が解けることを理解してもらえたと思います。今回お伝えしたルールや決まりをしっかりと覚えて次の単元に進んでください。
次は立体図形のポイント解説です。展開図を理解したうえで立体図形に進むことでより理解が深まります。

いかがだったでしょうか?回転体の問題は自力で回転体を書くことができればどんな問題がきても解けるということがわかってもらえたと思います。今回お伝えした「3ステップの書き方」をマスターして回転体の問題を解いてください。
最後までご覧いただきありがとうございました。
中学受験は算数や国語ではなく、「社会」の出来で合否が決まります!
そのため、第一志望に合格したいのであれば、社会を家庭学習でまず最初に固めるのが断トツの近道です!
【社会を最初に固めるべき理由】
● 算数の1点と社会の1点は、総合点で考えれば同じ1点
● 社会は暗記教科で学習センスがいらない!
● 社会は塾任せでは絶対に伸びない、家庭学習で伸ばす!
【短期間で社会の偏差値を上げたい方必見!】
短期間で偏差値を10以上アップさせた受験生多数!社会の偏差値を最速でアップできる社会に特化したスーパー教材を下記のページでご紹介しています!
\ 30日で社会の偏差値がアップ! /
スタディアップの教材はこちら
【たった5分で丸わかり】

