中学受験 算数 過不足算 ~面積図を使って問題を攻略~

中学受験の算数で出題される単元「過不足算」。ある個数のものを何人かに分けたりするとき、余りや不足が出る。この余りや不足から人数やあるものの個数を求めていきます。

過不足算は公式などはなく、暗記などの必要性はありませんが、文章を読解する力が問われます。個別に対策をしておかないと、試験で出題されたときに解くことがなかなか難しいです。

そこでこの記事では、面積図を使った過不足算の解き方を紹介します。「算数が苦手な人」「過不足算を初めて学習する人」「過不足算が苦手な人」でも理解しやすいように、分かりやすく解説しています。この記事を読むことで、過不足算とは何か理解でき、面積図を使った解き方を習得できるでしょう。

＼ 30日で社会の偏差値がアップ！ ／
スタディアップの教材はこちら
【たった5分で丸わかり】

過不足算① 基本問題

実際に例題を用いて過不足算の解き方を解説していきます。まずは自力で考えてから、解説を見るようにしてください。

例題1

飴玉を何人かの子どもに配ります。1人8個ずつ配ると、2個余ります。しかし10個ずつ配ると、10個足りません。子どもの人数は何人いますか。また、飴玉の数は何個あるか求めなさい。

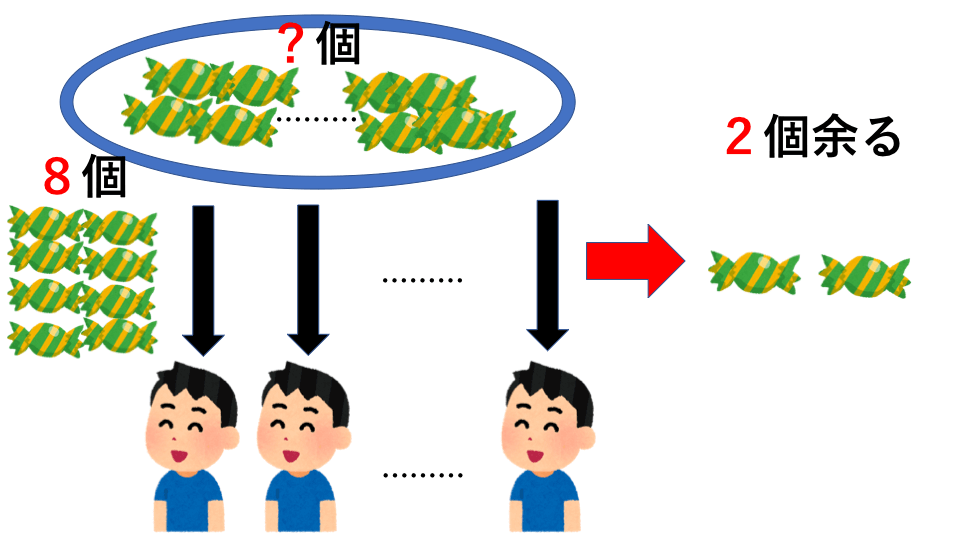
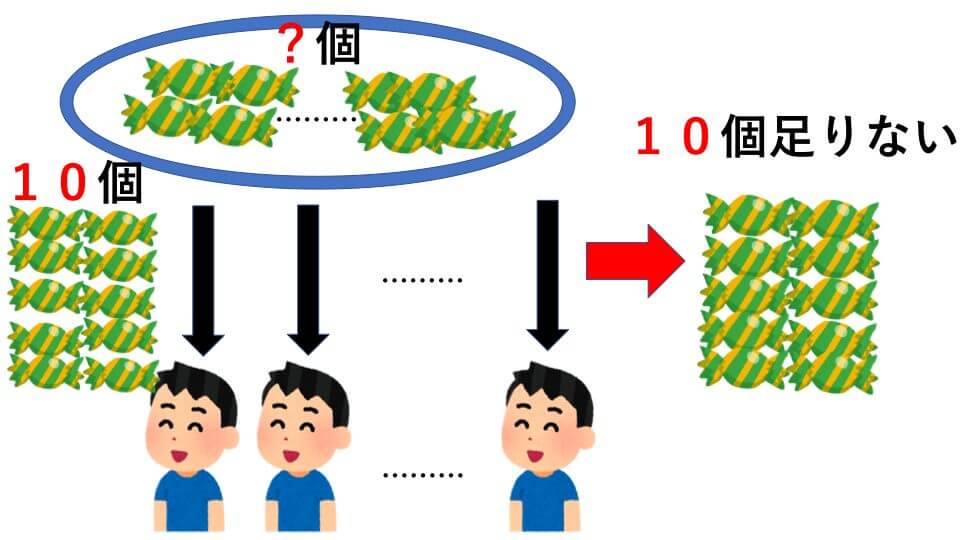
解説

下の図のように面積図書いて考えます。

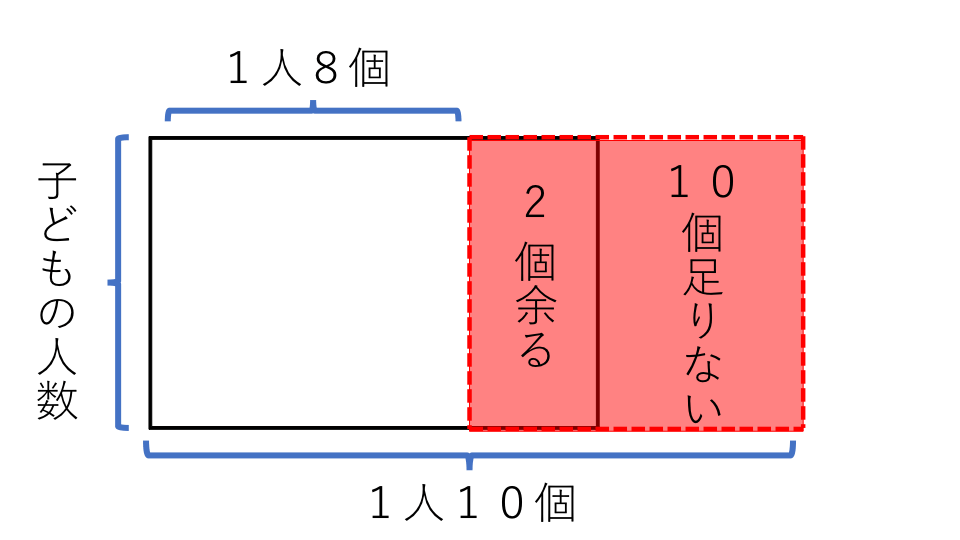
たては子どもの人数、横は1人に配る飴玉の個数、実線の長方形の面積は実際の飴玉の個数を表します。赤色の部分は全体の差となります。面積図をみてもらえばわかりますが、全体の差となる部分の飴玉の個数は(2＋10)個となります。つまり赤色の部分の面積は12として考えます。

赤色の面積のたての長さは子ども人数、横の長さは(10−8)となります。この(10−8)は一人分の差となります。

長方形の面積公式(たて×横＝面積)に当てはめて考えると、

□×2＝12 となります。この□は子どもの人数です。

この式を変形すると

□(子ども人数)＝12÷2＝6 となり

子どもの人数6人と分かります。

次に飴玉の個数を求めていきます。問題文の「1人8個ずつ配ると、2個余ります」という部分に注目して式を立てると、

飴玉の個数＝8×6＋2＝48＋2＝50

よって、答え　子ども人数6人、飴玉の個数50個

このように面積図を使って人数や個数を求めていきます。

例題2

子どもたちにえんぴつを配ります。1人に5本ずつ配ると、5本足りませんが、1人に4本ずつ配ると1本余ります。子どもの人数は何人いますか。またえんぴつの本数を求めなさい。

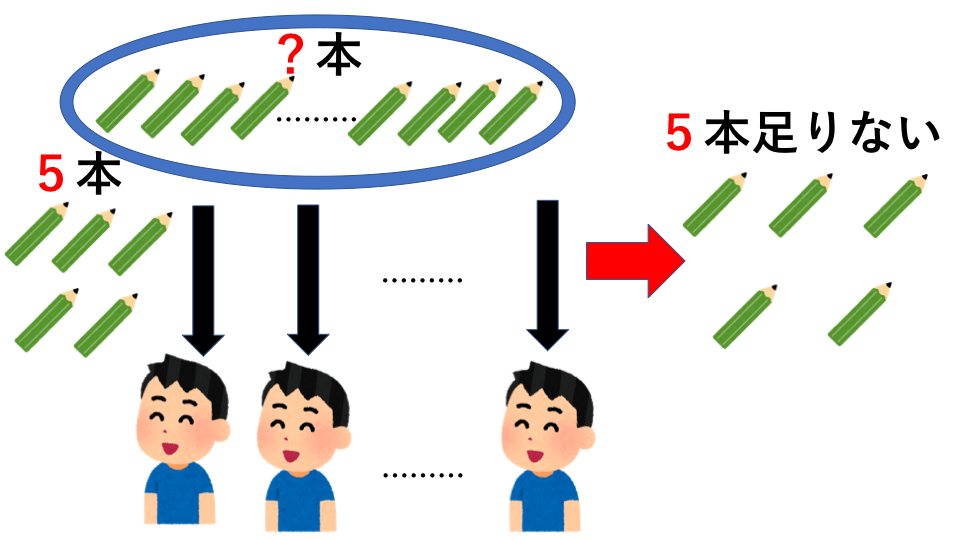
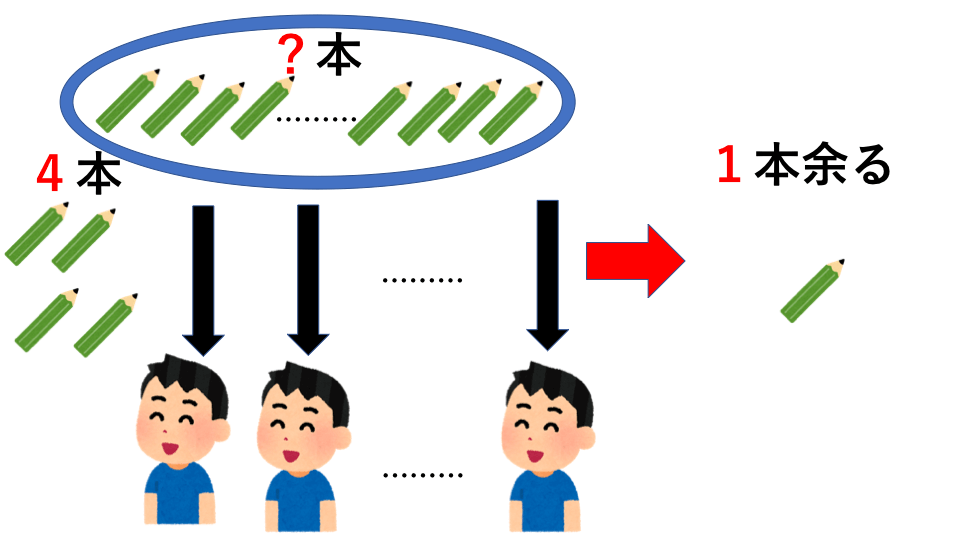
解説

まずは面積図に表して考えていきます。

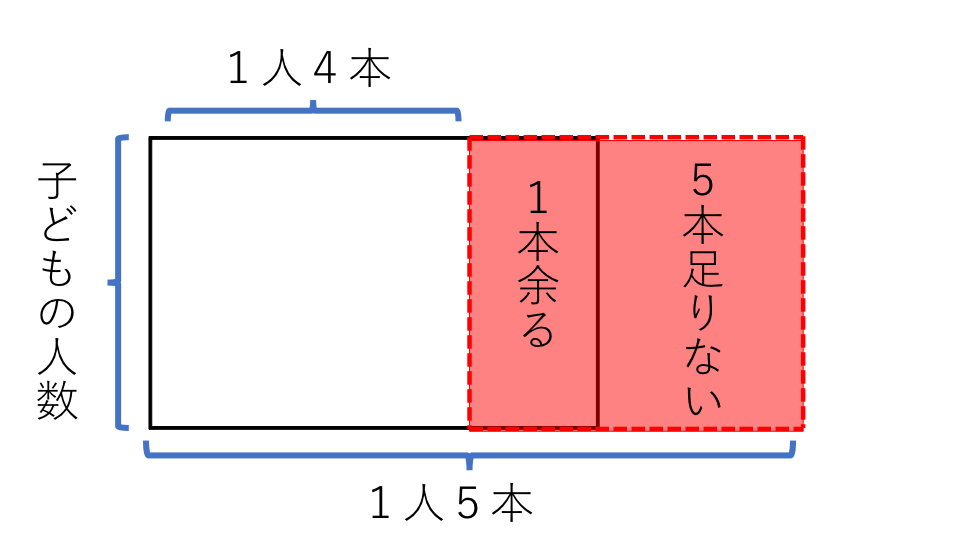
赤色の部分の面積(1＋5)が全体の差になります。この面積を利用して子どもの人数を求めていきます。面積は6、たての長さが子どもの人数、横の長さが1人分の差(5−4)となるので、子どもの人数を□とすると式は、

□×1 ＝6となり式を変形すると

□＝6÷1＝6となるので、

子どもの人数6人

次にえんぴつの本数を求めていきます。問題分の「1人に4本ずつ配ると1本余ります」という部分に注目して式を立てると、

えんぴつの本数＝6×4＋1＝25

よって、答え　子どもの人数6人、えんぴつの本数25本

過不足算② 応用問題

例題3

子どもたちに飴玉を配るのに、1人に8個ずつ配ると4個余りました。そこで、1人に9個ずつ配ったところ、1個しかもらえない子どもが1人、1個ももらえない子どもが1人いました。このときの子どもの人数と飴玉の個数を求めなさい。

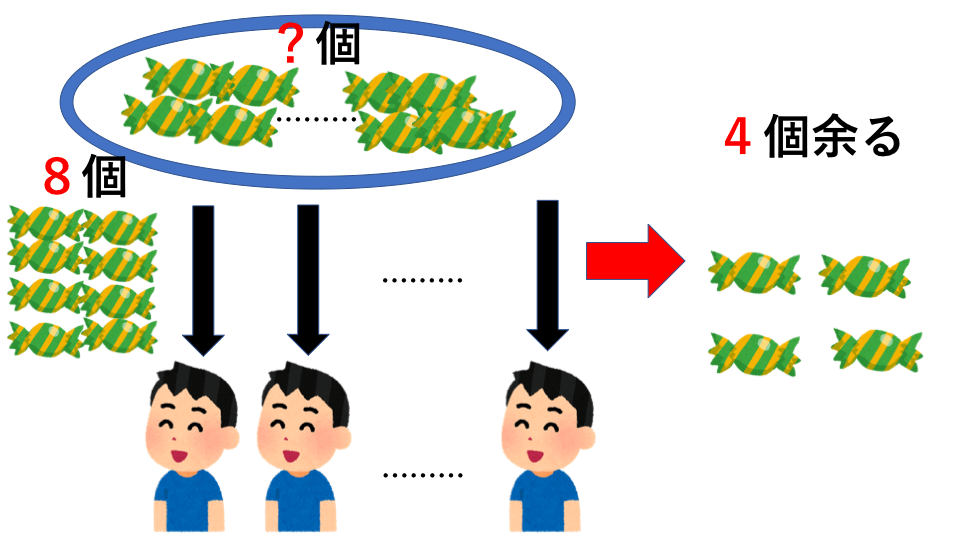
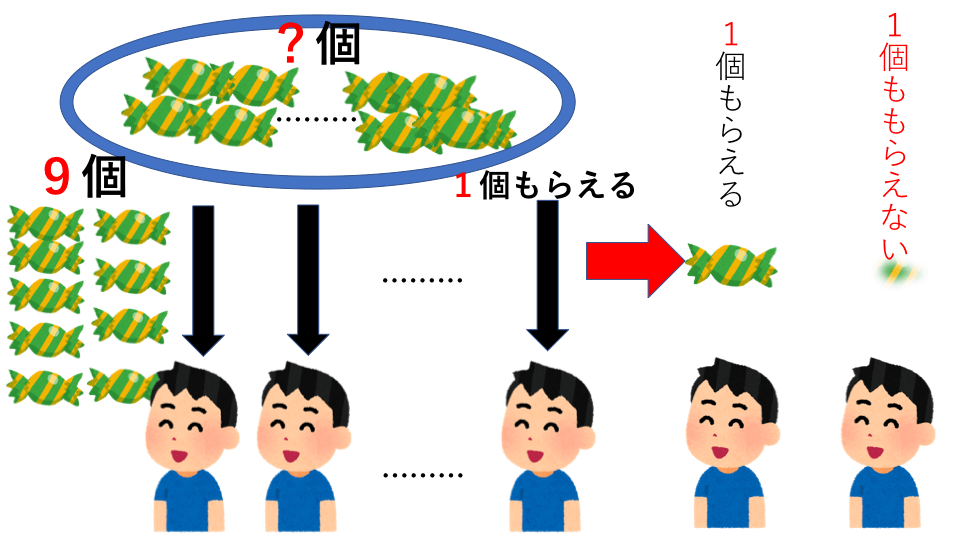
解説

少しひねりが加えられた問題です。まずは1人に9個ずつ配ったとき、何個足りないか考えます。

1個しかもらえない子どもが1人いるということは、この子ども1人には、

9−1＝8個足りないということになります。

また1個ももらえない子どもが1人いるので、この子ども1人には、

1×9＝9個足りないということになります。

つまり全体で8＋9＝17個足りないということがわかります。ですので、この問題は以下のように言い換えることができます。

子どもたちに飴玉を配るのに、1人に8個ずつ配ると4個余り、1人に9個ずつ配ると17個足りなくなりました。このときの子どもの人数と飴玉の個数を求めなさい。

すると、基本問題1と同じような問題になります。よって面積図を書いて考えていきます。

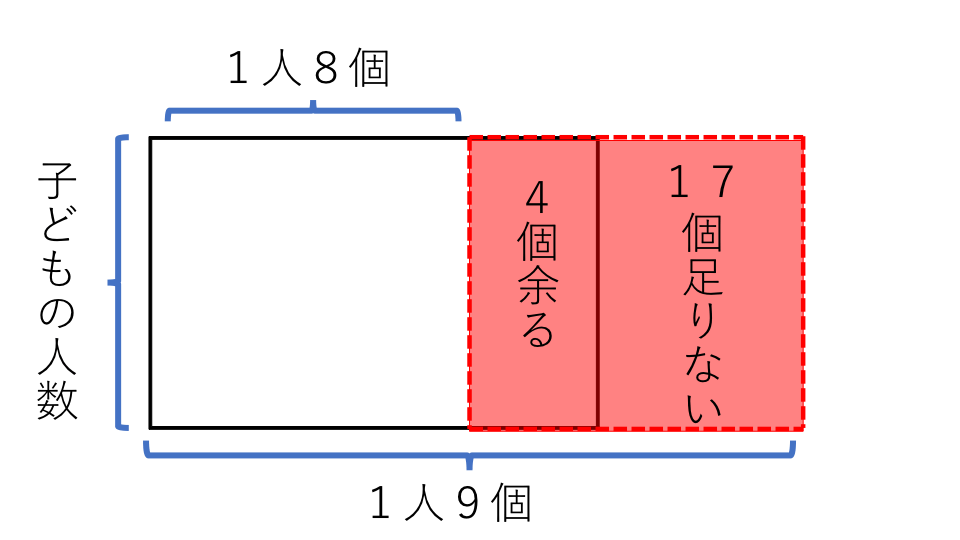
面積を用いて子どもの人数(たての長さ)を求めればいいので、

子どもの人数＝21÷1＝21

よって、子どもの人数21人

次に飴玉の個数を求めていきます。言い換えた問題文の「1人に8個ずつ配ると4個余り」の部分に注目して式を立てると、

飴玉の個数＝21×8＋4＝172

よって、答え　子どもの数21人、飴玉の個数172個

この問題のように、問題文を言い換えて解く問題も出題されます。

例題4

太郎さんは家から学校まで行きます。分速100mで歩くと予定時間に5分遅れます。しかし分速200mで走ると予定時間より5分早く学校に到着します。家から学校までは何kmありますか。また予定時間も求めなさい。

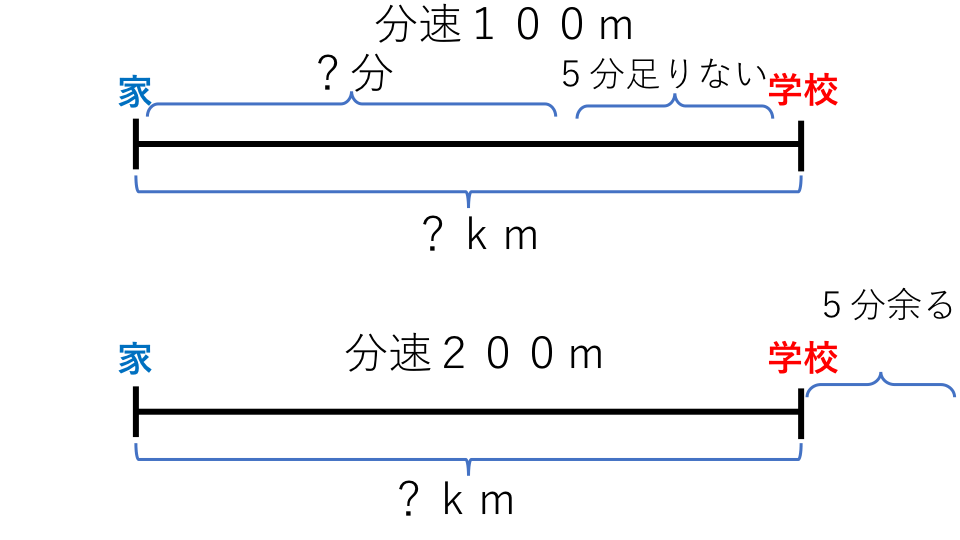
解説

面積図を書いて考える前に、過不足がどれだけあるのか考えます。

分速100mで歩くと予定時間に5分遅れるということは

「100×5＝500mの不足」、分速200mで走ると予定時間より5分早く到着するということは「200×5＝1000mの余り」ということになります。ですので面積図を考えると下のようになります。

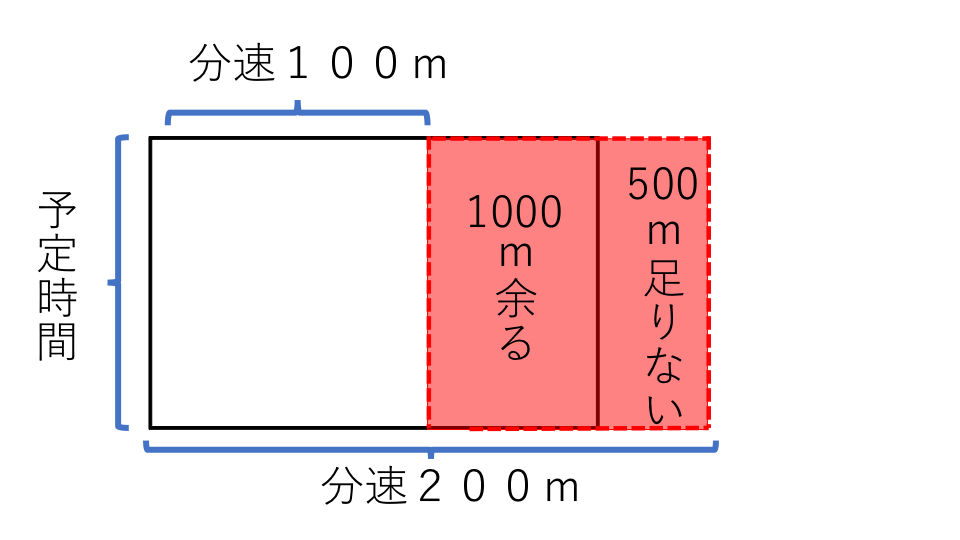
面積を用いて予定時間(たての長さ)を求めればいいので、

予定時間＝(1000＋500)÷(200−100)＝15分

家から学校までの距離は問題文の「分速100mで歩くと予定時間に5分遅れます」という部分に注目して式を立てると、

家から学校までの距離＝100×(15＋5)＝2000(m)

ここで出た答えの単位はmなのでkmに直すと2km

よって、答え　予定時間15分、家から学校までの距離2km

まとめ

いかがだったでしょうか？問題文をよく読んで過不足がいくつあるのか考えて、面積図を書くことで簡単に解けることがわかってもらえたと思います。本番でも面積図を書いて考えるようにしてください。

次は分配算のポイント解説です。過不足算を理解した上で分配算に進むことでより理解が深まります。

＼ 30日で社会の偏差値がアップ！ ／
スタディアップの教材はこちら
【たった5分で丸わかり】