中学受験 算数 分配算 ~線分図を使った解き方でわかりやすく解説~

中学受験の算数で出題される単元「分配算」。あるものを配ったり、分けたりするときに、それぞれの数量をそれらの和、差、比などを利用して求めます。

分配算では特に覚える公式などはなく、問題文をよく理解し論理的に出題者の意図を捉える思考能力が試される問題となっています。

しかし、分配算にも似たような問題やパターンがあるので、それらを事前に学習することによって、解きやすくなりますし、試験当日に出題された場合でも慌てることはありません。

この記事では、そんな線分図を使った分配算の解き方を紹介します。算数が苦手な人や分配算数を初めて学習する人、分配算が苦手な人でも理解しやすいように、わかりやすく解説しています。この記事を読むことで、分配算とは何か理解でき、線分図を使った解き方を習得できます。

＼ 30日で社会の偏差値がアップ！ ／
スタディアップの教材はこちら
【たった5分で丸わかり】

分配算① 基本問題

実際に例題を用いて分配算の解き方を解説していきます。まずは自力で考えてから、解説を見るようにしてください。

例題1

兄弟2人でお母さんから飴玉をもらいました。お兄さんは弟の2倍よりも2個多くもらい、2人合わせて62個の飴玉をもらいました。このときのお兄さんと弟の飴玉の個数を求めなさい。

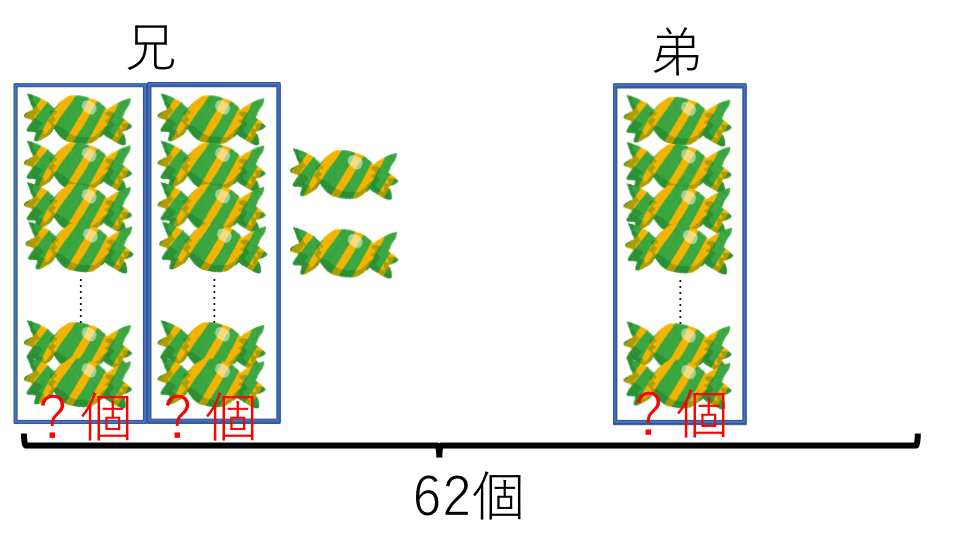
解説

この手の問題の考え方は、問題文を読んで線分図に表してから考えていきます。弟のもらった飴玉の個数を①として2人がもらった飴玉の個数の関係を線分図に表すと下の線分図のようになります。

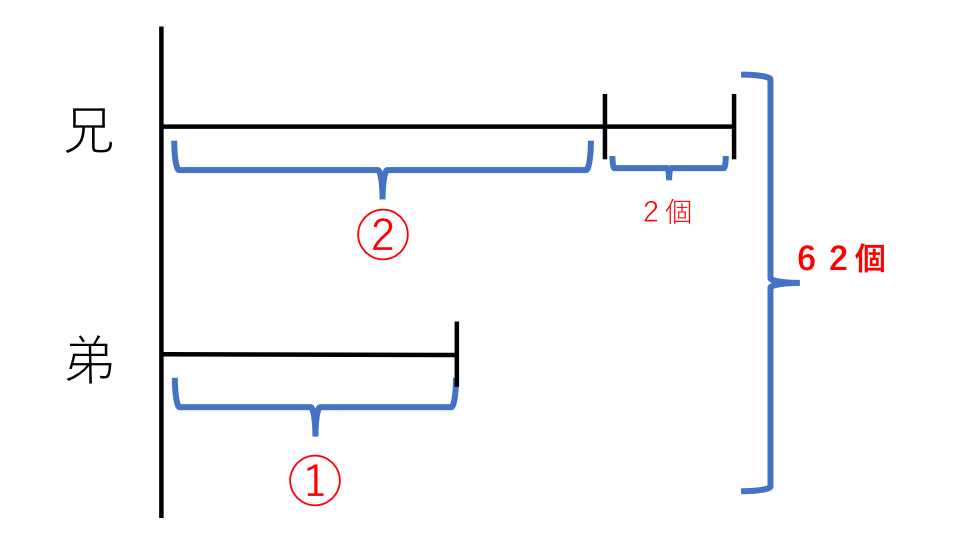
②は弟の2倍の数を表しています。

合計の62個から兄がもらっている分の2個を引くと残りは

①＋②＝③となります。ですので③の個数は

③＝62−2＝60(個)

③は①の3倍なので、①の個数は③÷3＝①で求めることができます。よって

①＝60÷3＝20 (個)

これで弟の個数が求めることができました。次はお兄さんの個数を求めていきます。

問題文の「お兄さんは弟の2倍よりも2個多くもらい」という部分に注目して、数式に表すと、

(20×2)＋2＝42(個)

よって、答え　お兄さんの飴玉42個、弟の飴玉20個

例題2

8000円を兄弟で分けます。次のように分けるとき、2人の取り分はそれぞれいくらになるか求めなさい。

(1)お兄さんの金額が弟の4倍より500円多くなるように分けるとき。

(2)お兄さんと弟の金額の比率が5:3となるように分けるとき。

解説

(1)から解説していきます。まずは弟の取り分を①として、2人の取り分の金額の関係を線分図に表して考えます。線分図は下のようになります。

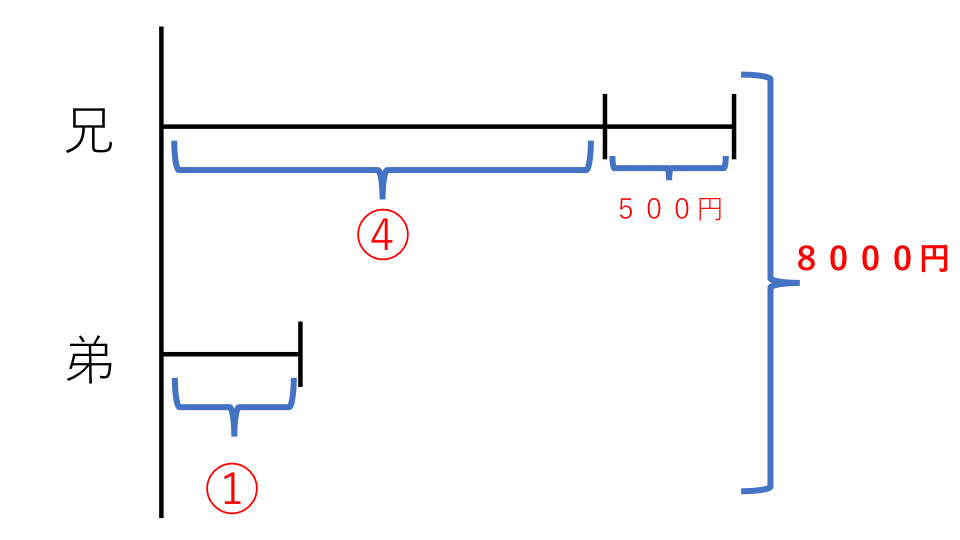
④は①の4倍であることを示しています。

合計の金額8000円から兄がもらっている500円分を引くと残りは

①＋④＝⑤となります。ですので⑤の金額は

⑤＝8000−500＝7500(円)

⑤は①の5倍なので、①の金額は⑤÷5で求めることができます。よって

①＝7500÷5＝1500(円)

これで弟の金額がわかりました。次はお兄さんの金額を求めていきます。

問題文の「お兄さんの金額が弟の4倍より500円多くなる」に注目して数式に表すと、

(1500×4)＋500＝6500(円)

よって、答え　お兄さんの取り分6500円、弟の取り分1500円

(2)はすでに比率が決められているので、この比率に従って線分図を書いていきます。すると線分図は下のようになります。

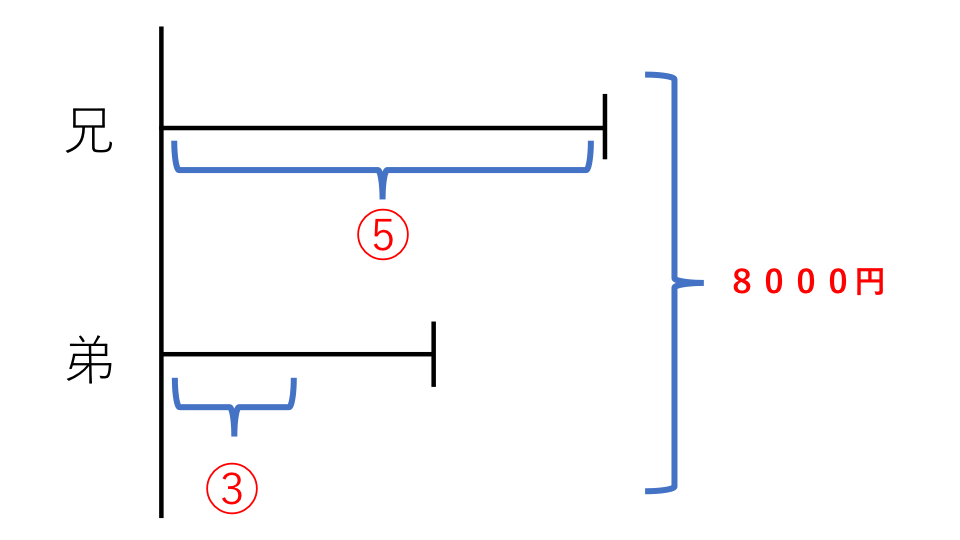
合計の金額が8000円なので、合計の金額は

⑤＋③＝⑧と表すことができます。

⑧は①の8倍なので①は

①＝8000÷8＝1000(円)とわかります。

⑤は①の5倍、③は①の3倍なのでそれぞれの金額は、

⑤＝1000×5＝5000(円)

③＝1000×3＝3000(円)

よって、答え　お兄さんの取り分5000円、弟の取り分3000円

例題3

245個の飴玉をA君、B君、C君の3人で分けました。A君はB君の3倍多くもらい、C君はB君の2倍よりも5個多くもらいました。このときの、A君、B君、C君はそれぞれ飴玉を何個もらったか求めなさい。

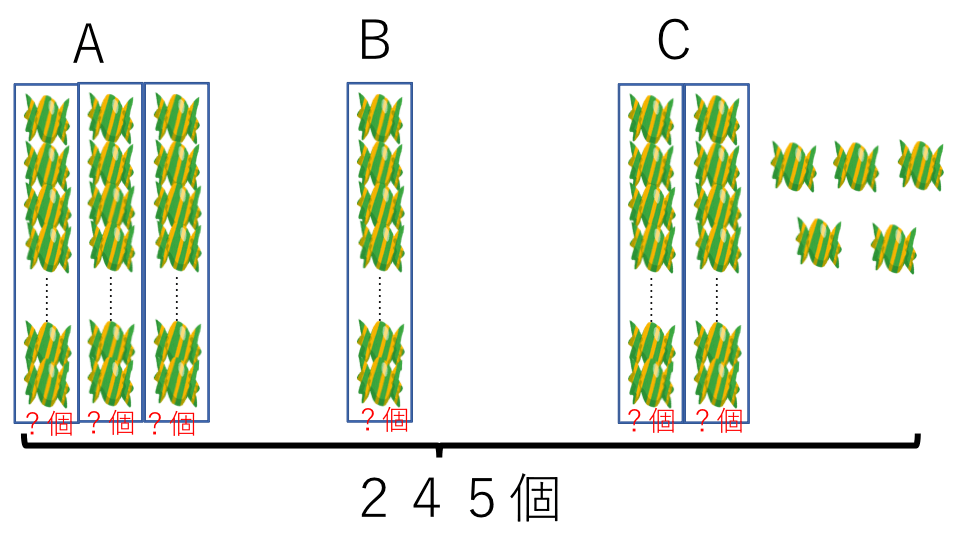
解説

3人になっても線分図を書いて考えていきます。問題文を読んでもらうと分かると思いますが、すべての基準がBくんとなっているので、B君のもらった飴玉の個数を基準として考え①とします。3人のもらった飴玉の個数の関係を線分図に表すと下の図のようになります。

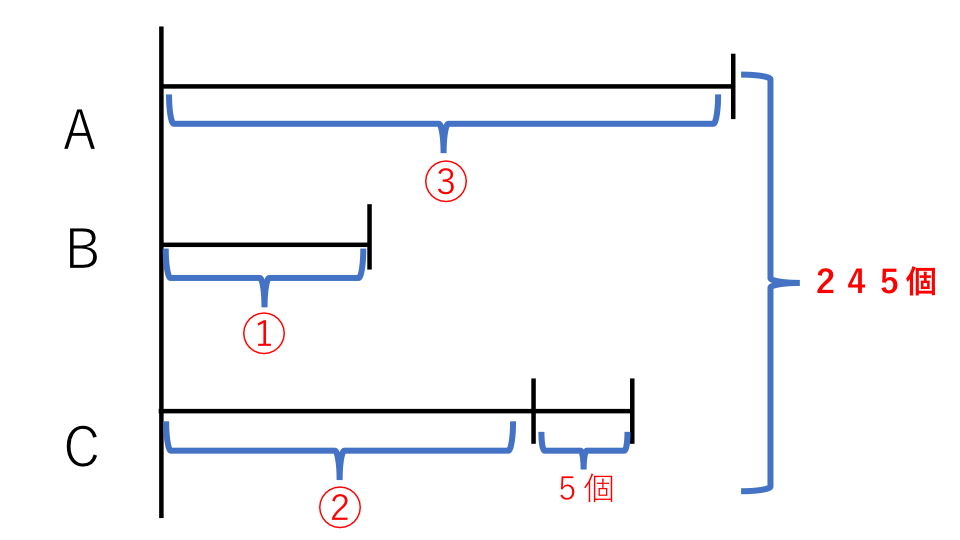
合計の245個からC君がもらっている5個を引くと、残りは③＋①＋②＝⑥となります。⑥の個数は

⑥＝245−5＝240(個)となります。

⑥は①の6倍なので①の個数は、

①＝240÷6＝40(個)となります。

続いて③は①の3倍なので、③の個数は、

③＝40×3＝120(個)

C君の個数は、問題文の「C君はB君の2倍よりも5個多くもらいました」という部分に注目して数式に表して考えると、

40×2＋5＝85(個)

よって、答え　A君120個、B君40個、C君85個

分配算② 応用問題

例題4

2つの整数があります。その和は452です。また大きい方の数を小さい方の数で割ると、商が7であまりが36になります。このときの2つの整数を求めなさい。

解説

今までの基本問題と同様に線分図を使って考えていきますが、少し捻られた問題で難しいです。商品が7であまりが36ということは、大きい方の数は小さい方の数の7倍で36大きい数と言い換えることができます。

これを利用して線分図に表すと下の図のようになります。

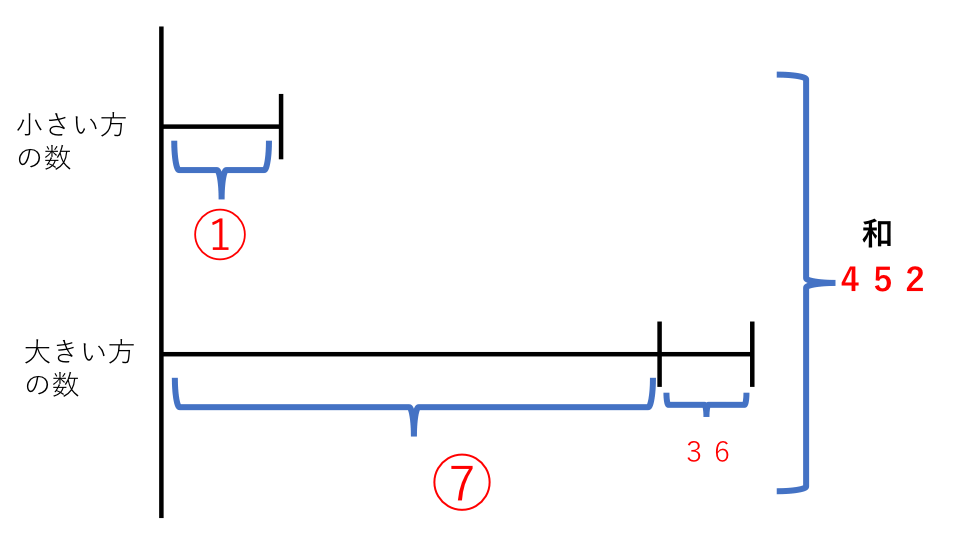
小さい数を基準として①としました。

全体の和452から36を引くと、残りは①＋⑦＝⑧となります。⑧の数は

⑧＝452−36＝416となります。

⑧は①の8倍の数なので、①の数は、

①＝416÷8＝52

次に大きい方の数を求めていきます。大きい方の数は小さい方の数の7倍で36大きい数字です。これを数式に表すと、

52×7＋36＝400

よって、答え　400と52

まとめ

いかがだったでしょうか？問題文をよく読んで線分図書くことで、答えが導き出せることがわかってもらえたと思います。

しかし線分図が書けても、そこからどうするか分からなければ意味がありません。ですので、分配算の問題を多く解いて線分図からどのようにして導き出すことができるのか理解できるようにしておきましょう。

＼ 30日で社会の偏差値がアップ！ ／
スタディアップの教材はこちら
【たった5分で丸わかり】

次は平均算のポイント解説です。分配算を理解した上で平均算に進むことでより理解が深まります。