中学受験の算数で出題される単元「平均算」。個数や合計から平均を求めたり、平均から個数や合計を求めたりします。
平均算は考え方は単純ですが、計算量が多くなる場合が多く、ミスをしやすい単元です。今まで学習した算数の力が試される単元でもあります。
また平均算は日常生活でも使いますし、中学校の数学の単元でも学習します。ですので平均算の単元はこれからの基礎となるので十分に理解しておきたい単元です。
この記事では、面積図を使った平均算の解き方を中心に解説していきます。「算数が苦手な人」「平均算を初めて学習する人」「平均算が苦手な人」でも理解しやすいようにわかりやすく解説しています。この記事をご覧になることで、平均算とは何か理解でき、面積図を用いた計算方法がわかるようになります。
中学受験は算数や国語ではなく、「社会」の出来で合否が決まります!
そのため、第一志望に合格したいのであれば、社会を家庭学習でまず最初に固めるのが断トツの近道です!
【社会を最初に固めるべき理由】
● 算数の1点と社会の1点は、総合点で考えれば同じ1点
● 社会は暗記教科で学習センスがいらない!
● 社会は塾任せでは絶対に伸びない、家庭学習で伸ばす!
【短期間で社会の偏差値を上げたい方必見!】
短期間で偏差値を10以上アップさせた受験生多数!社会の偏差値を最速でアップできる社会に特化したスーパー教材を下記のページでご紹介しています!
\ 30日で社会の偏差値がアップ! /
スタディアップの教材はこちら
【たった5分で丸わかり】
平均算① 平均算とは
いくつかの数や量を、同じ大きさになるようにならしたものを、それらの数や量の平均と言います。
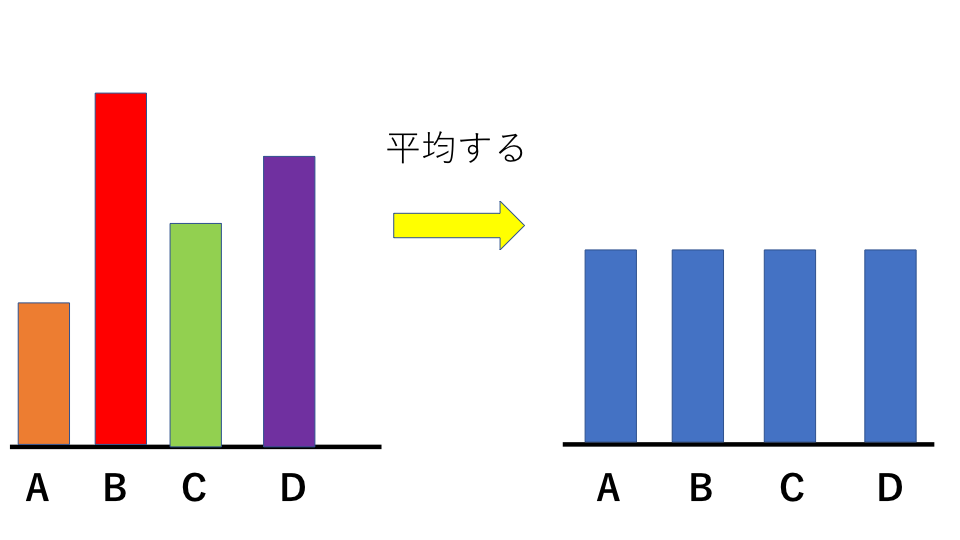
上の図のように、不特定にある数をならすことです。
平均は、いろいろな大きさをもったいくつかの数や量の集まりを1つの数や量で代表させたものとも言うことができます。
平均を求めるためには、いくつかの数や量の合計を、それらの個数で割ります。そのとき出る平均は整数ではなく、小数や分数になるときもあります。
例えば、4人のテストの点数が、8点、9点、7点、10点のとき、これらの点数の平均は、
(8+9+7+10)÷4=8.5(点)
平均=合計÷個数
平均算② 基本問題
例題1
算数のテストを5回受けました。それぞれの結果が、80点、85点、70点、90点、82点でした。6回目のテストで何点をとると6回のテストの平均点が80点になりますか?
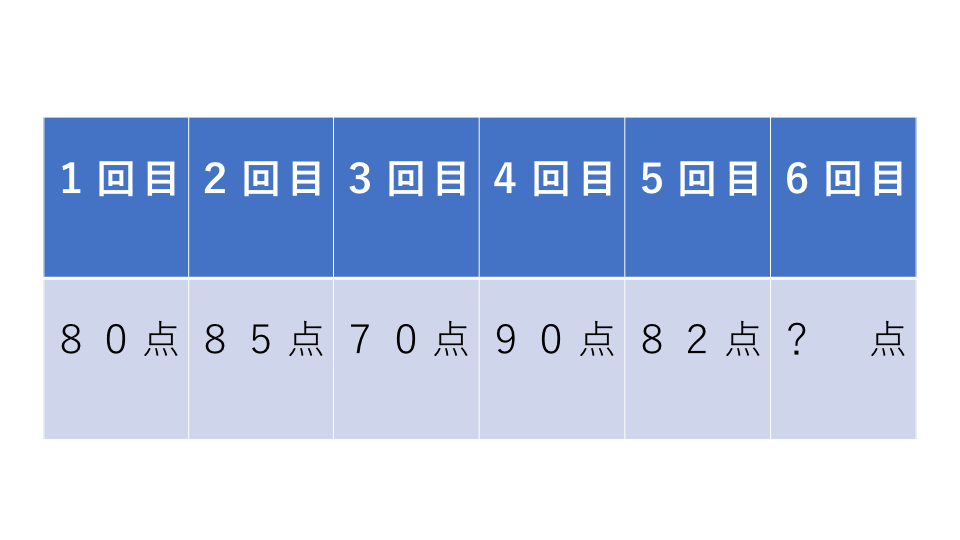
解説
平均点と回数から合計点数を求めて考えていきます。
まずは5回目までわかっているので、5回目までの合計の点数を求めると、
80+85+70+90+82=407(点)
次に、6回のテストの平均点が80点になるときの合計の点数を求めると、
80×6=480(点)
ここから、5回目の時点で407点なので、6回目で合計点数が480点になるような点数を6回目でとれば、平均点が80点になると言うことがわかるので、6回目の点数は、
480-407=73(点)
よって、答え 73点
例題2
男子15人、女子12人のクラスで算数のテストをしました。男子の平均点が70点、クラス全体の平均点が75点でした。このとき女子の平均点は何点か求めなさい。
解説
男子の合計点数とクラス全体の合計点数を使って、女子の平均点を求めていきます。
クラス全体の人数は、男子と女子の合計の人数なので、
15+12=27(人)
クラス全体の平均点は75点なので、クラス全体の合計点数は、
75×27=2025(点)
次に男子の合計点数を求めます。男子の平均点は70点で人数は15人なので、
70×15=1050(点)
クラス全体の合計点数と男子の合計点数の差が女子の合計点数になるので、
2025-1050=975(点)
女子の合計点数は975点、人数は12人なので、女子の平均点は、
975÷12=81.25(点)
よって、答え 81.25点
平均算③ 面積図を使った問題
例題3
あるクラスで算数のテストを行いました。その結果、男子15人の平均点が80点、女子の平均点が90点、クラスの平均点が85点でした。このクラスの女子は何人いるか求めなさい。
解説
次の手順で面積図を書いて、問題の答えを考えていきます。
たて80点、横15人の長方形を書きます。この長方形の面積は男子の合計点数です。
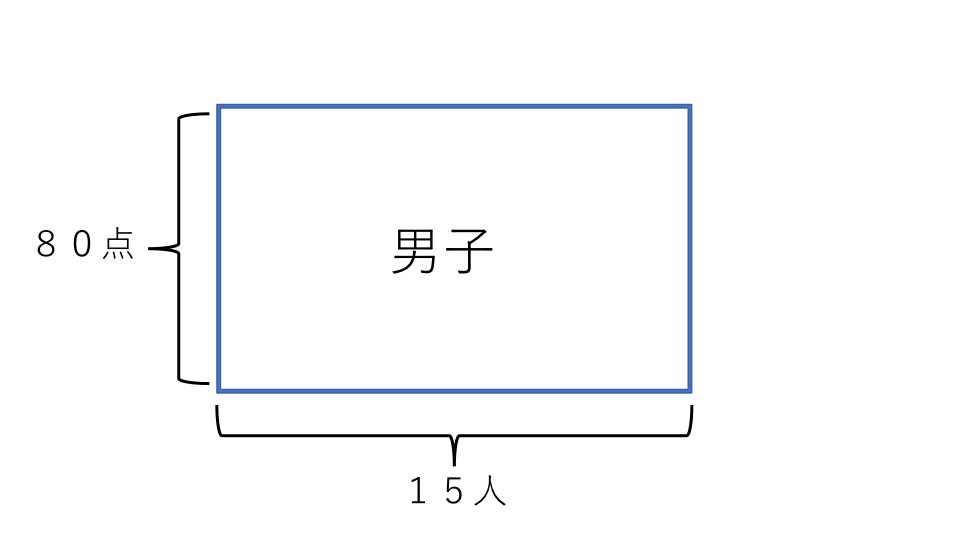
次に先ほど書いた男子の長方形の横に、たて90点、横X人の長方形を書きます。女子の人数はわからないのでX人とします。この長方形の面積は女子の合計点数です。
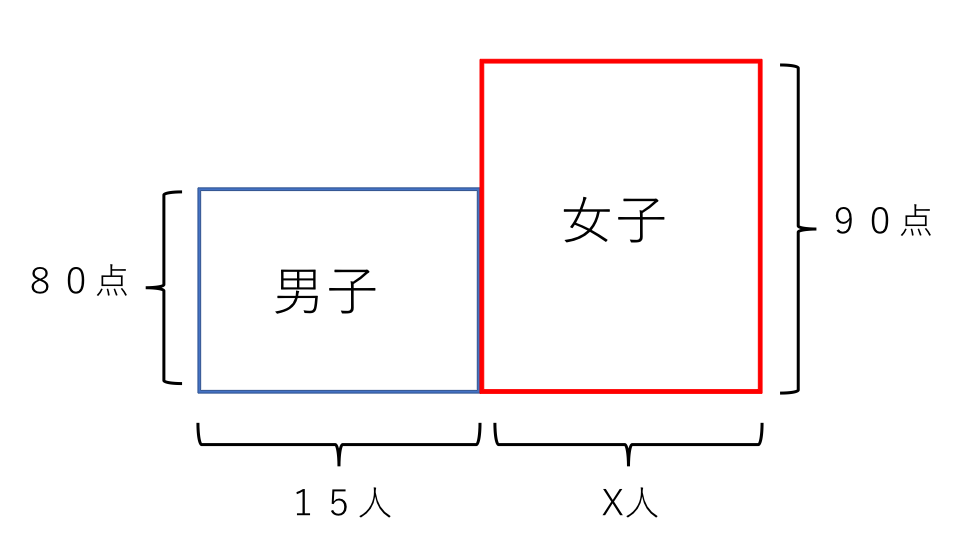
最後に女子と男子の長方形のたての長さをそろえます。この長方形のたての長さはクラスの平均点です。
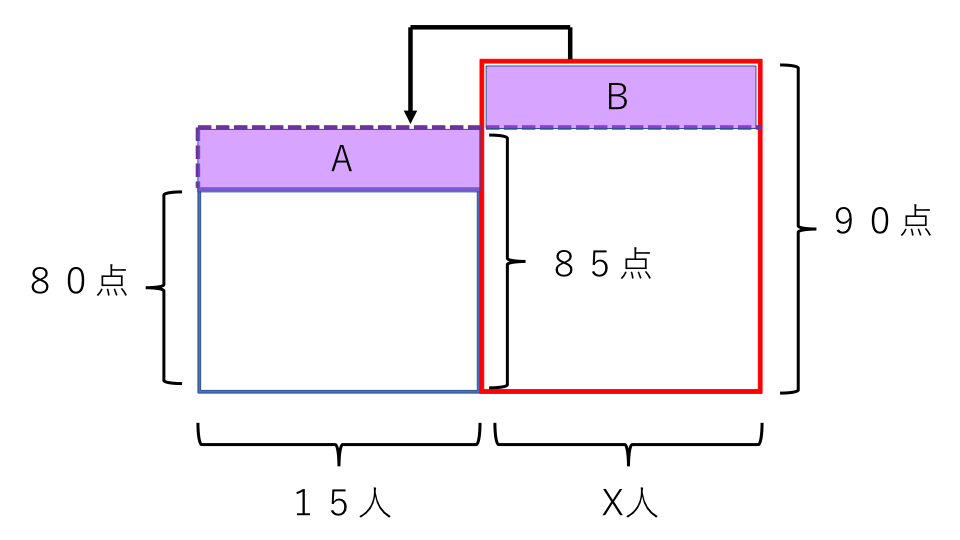
上の図で、長方形Aと長方形Bの面積は等しくなります。長方形Aと長方形Bの面積の関係を式に表すと、
(85-80)×15=(90-85)×X
75=5×X
X=15
よって、答え 15人
例題4
あるクラスのマラソン大会の記録を調べました。男子12 人の平均完走時間が50分、女子の平均完走時間が45分、クラスの平均完走時間が47分でした。このクラスの女子は何人いるか求めなさい。
解説
先程の問題と同じように面積図を書いて考えていきます。
たて50分、横12人の長方形を書きます。このときの長方形の面積は男子の合計完走時間です。
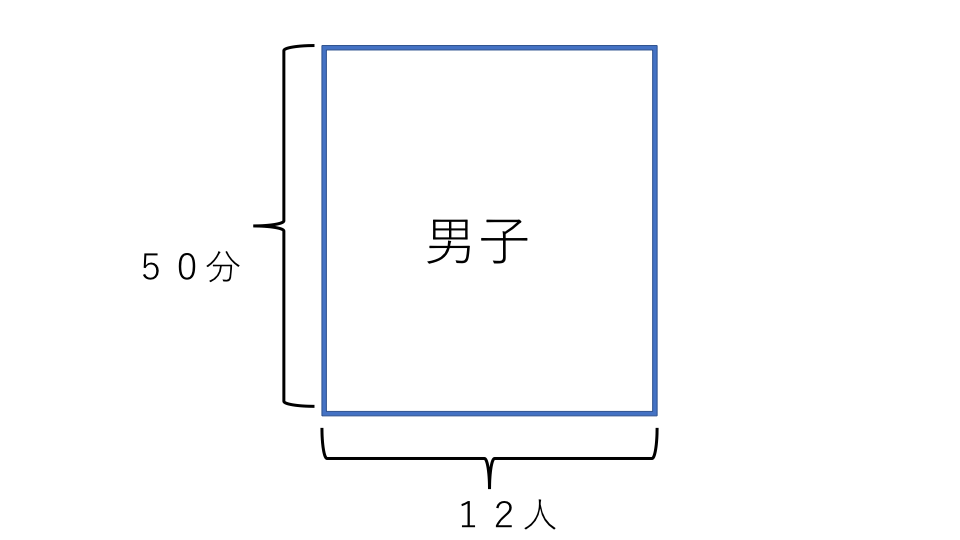
次は先ほどの作った男子の長方形に、たて45分、横X人の長方形を書きます。女子の人数はわからないのでX人とします。この長方形の面積は女子の合計完走時間です。

女子と男子の長方形のたての長さをそろえます。この長方形のたての長さはクラスの平均完走時間になります。
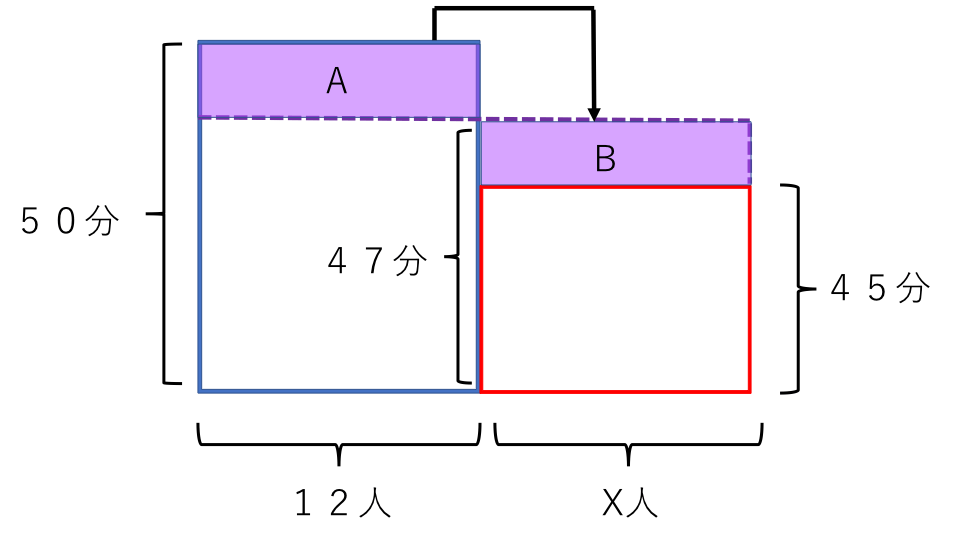
この図の長方形Aと長方形Bの面積は等しくなります。長方形Aと長方形Bの面積の関係を式に表すと、
(50-47)×12=(47-45)×X
36=2×X
X=18
よって、答え 18人
例題5
ある学校の入学試験で、受験生全体の平均点は50点でした。また合格者の人数は120人、不合格者の人数は200人で、合格者の平均点は不合格者の平均点より15点高かったそうです。このときの不合格者の平均点を求めなさい。
解説
先程の問題とは少し違いますが、同じように面積図を用いて答えを求めていきます。
たてX点、よこ120人の長方形を書きます。この長方形の面積は合格者の合計点数です。
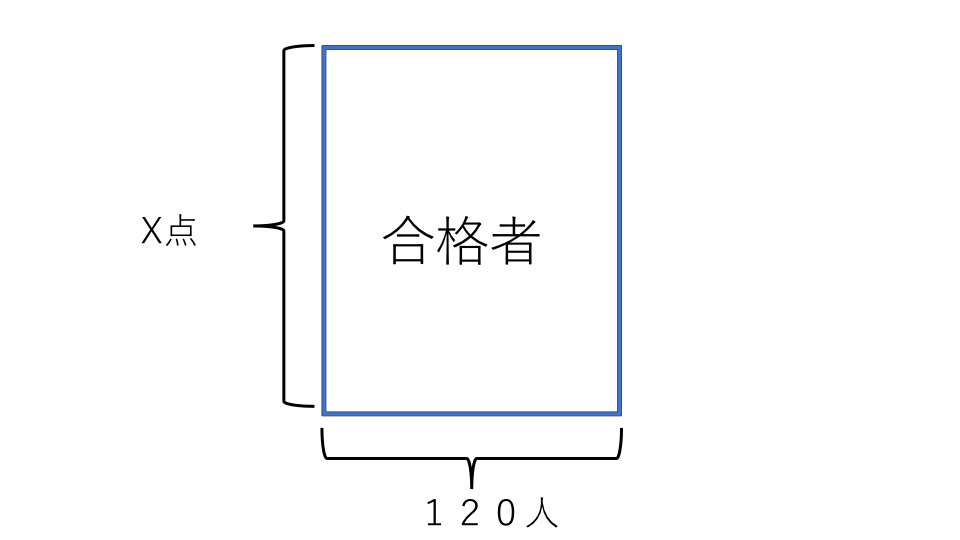
合格者の長方形の横に、たてY点、よこ200人の長方形を書きます。この長方形の面積は、不合格者の合計点数です。
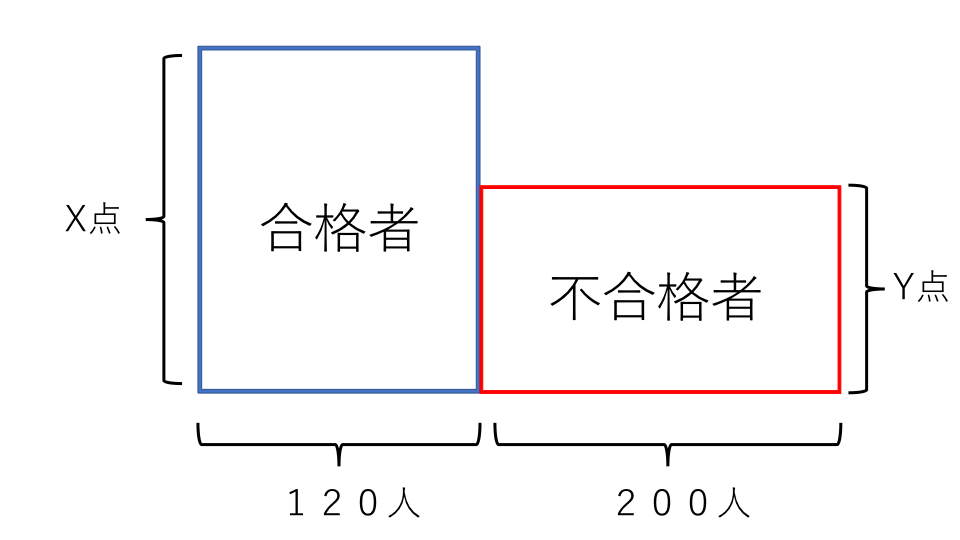
合格者と不合格者のたての長さをそろえます。
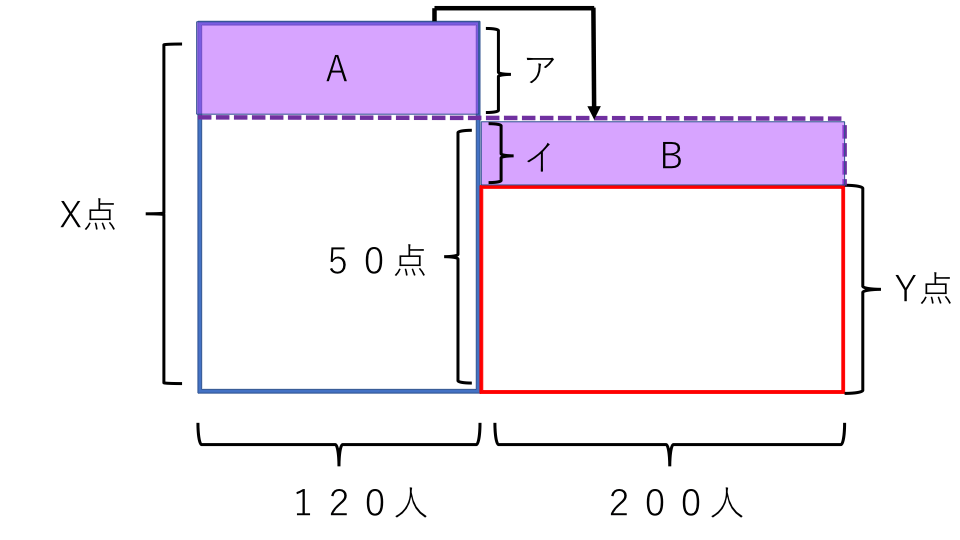
長方形Aと長方形Bのの面積は等しいので、アとイの長さの比は120:200の逆比のなります。ですので、
(アの長さ):(イの長さ)=200:120=5:3 となります。
アとイの長さの合計は15点なので、イの長さは、
イ=15×3/5+3=45/8=5.625(点)
ですので、Yの点数は、
Y=50-5.625=44.375(点)
よって、答え 44.375点
まとめ
いかがだったでしょうか?
計算量が多く難しかったと思いますが、考え方自体はそこまで難しくなかったと思います。
平均算の難しい問題では面積図を書いて考えると大抵の問題は解くことができます。今回学習した面積図の書き方をしっかりと理解して、問題をどんどん解いていってください。
中学受験は算数や国語ではなく、「社会」の出来で合否が決まります!
そのため、第一志望に合格したいのであれば、社会を家庭学習でまず最初に固めるのが断トツの近道です!
【社会を最初に固めるべき理由】
● 算数の1点と社会の1点は、総合点で考えれば同じ1点
● 社会は暗記教科で学習センスがいらない!
● 社会は塾任せでは絶対に伸びない、家庭学習で伸ばす!
【短期間で社会の偏差値を上げたい方必見!】
短期間で偏差値を10以上アップさせた受験生多数!社会の偏差値を最速でアップできる社会に特化したスーパー教材を下記のページでご紹介しています!
\ 30日で社会の偏差値がアップ! /
スタディアップの教材はこちら
【たった5分で丸わかり】

