【中学受験 算数】 等差数列・等比数列・階差数列の重点ポイントまとめ

中学受験の算数で出題される単元「等差数列」「等比数列」「階差数列」。この単元では、規則性の把握が求められます。算数は論理的に物事を考える能力を身に付けるための学問ですが、等差数列・等比数列・階差数列の問題は、まさしくこの論理的思考が求められる問題であると言えます。

もともと、これらの数列に関する問題は小学校では教育範囲に入っておらず、中学の「数学B」で習う範囲です。しかし中学受験の算数では考え方を中心に出題されるためしっかり学習しておきましょう。

この記事でお伝えする内容は、おそらく小学校では通常、習わないやり方だと思います。小学校で習う範囲で解くことも可能ですが、公式や仕組みを知っておくことで、中学受験に有利に進められるので、必ず覚えて入試本番に挑んでください。「規則性についての問題がよくわからない」「数列てそもそも何？」という人はこの記事を読むことで、規則性の問題、数列の問題は楽に解けるようになるでしょう。

＼ 30日で社会の偏差値がアップ！ ／
スタディアップの教材はこちら
【たった5分で丸わかり】

そもそも数列って何？

数列とは「ある決まりによって数を規則的に並べたもの」のことを言います。小学校では規則性の問題として習うと思います。

具体的に例を挙げると

1， 2，3，4，5，6，7，8…

これは数値が1ずつ大きくなっていっていますよね。

1，3，5，7，9，11，13…

これは数値が2ずつ大きくなっていっています。13の次にくる数値は15だと予測ができます。

2，4，8，16，32，64，128…

これは次の値がとなりの数値2倍になっています。
ですので、次にくる数値は256だと予測できます。

このようにある規則性に従って並んだ数字を見つけたら、数列の問題と思ってください。数列の1番最初の数字のことを第1項または初項、2番目の数字のことを第2項といいます。これから「項」という言葉がよく出てくるので、意味を十分に理解してください。

等差数列

等差数列とは差が等しい数列のことを指します。

先程例に挙げた　1，3，5，7，9，11，13…

これは初項が1で、それから2ずつ増えていっています。

2ずつ増えていくということは「差」が2ということになります。
この時の「差」のことを「公差」と言います。この数列は初項1、公差2の等差数列と言えます。

次のような問題が出題されたとします。

例題1

1，5，9，13，17，21… この等差数列の初項と公差を求めなさい

解説

初項は一番初めの数字のことなので、1 。公差は前の数字との差なので、見てみると4ずつ増えていっているのが分かります。なので公差は4というふうになります。

○番目の数を求める問題

例題2

1，6，11，16，21，26…

この数列の15番目の数値を答えなさい。

解説

いきなり15番目の数字を考えるのは難しいので、すでに答えがわかっている6番目の数字を使って考えます。

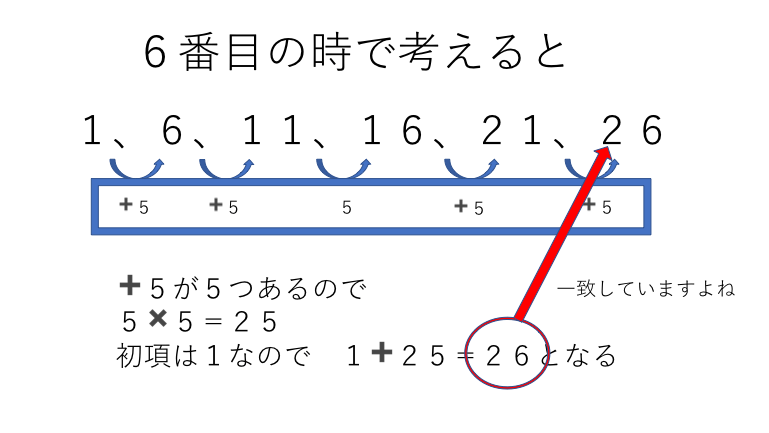
上の図のように6番目の数字まで(＋5)が5回あることがわかります。ですので、最初の数字から5を5回足した数字が6番目の答えになるので、式は1＋(5×5)＝26 となります。一致しましたよね。

ではこの考え方を使って15番目の数字を考えていきます。下の図を見てください。

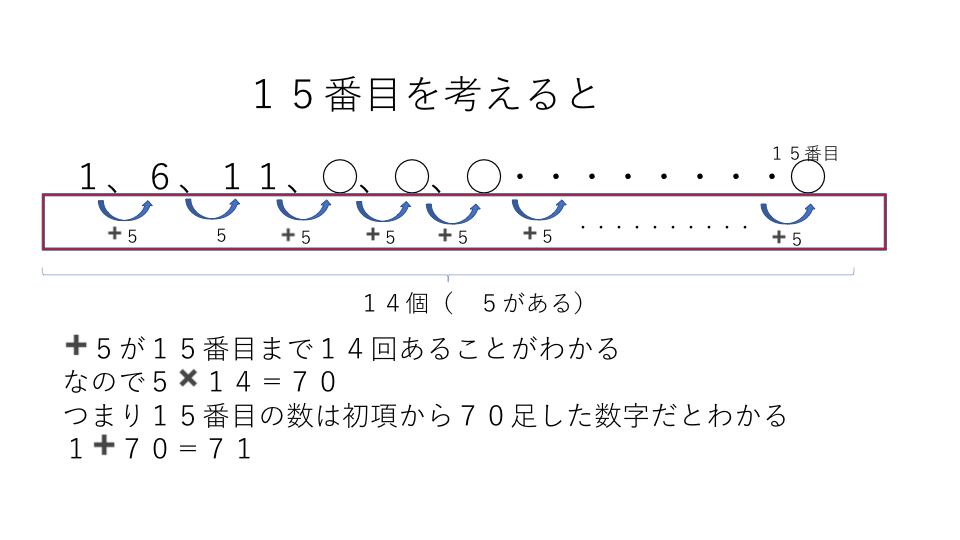
15番目までは(＋5)が14回足されていることが分かると思います。ですので、15番目数字は初項から(＋5)が14回足された数字になるので式は1＋(5×14)＝71 　　答え71となります。

数列はこのように書いて理解して答えを導き出します。しかし毎回このように考えていると時間がかかってしまいます。そこで次のような公式があります。

となります。この公式の原理は先程の例題2で説明したことから成り立ちます。
ただ単に公式だけを覚えて使うと、公式の意味を理解できず、公式を忘れてしまったり、応用問題になった時に解くことができません。ですので、公式をただ単に覚えることはやめましょう。

先程の問題を公式を使って解くと、初項1、公差5ですので

1＋5×(15-1)＝1＋5×14＝71 となります。

○番までの和

例題3

次のような数列の1番目から10番目までの和を求めなさい　1，5，9，13，17，21…

解説

下の図のように10番目まで書いて求めるのは時間がかかり、計算ミスもしやすくなります。

ですのでこのやり方はおすすめしません。
どのように考えるかというと、

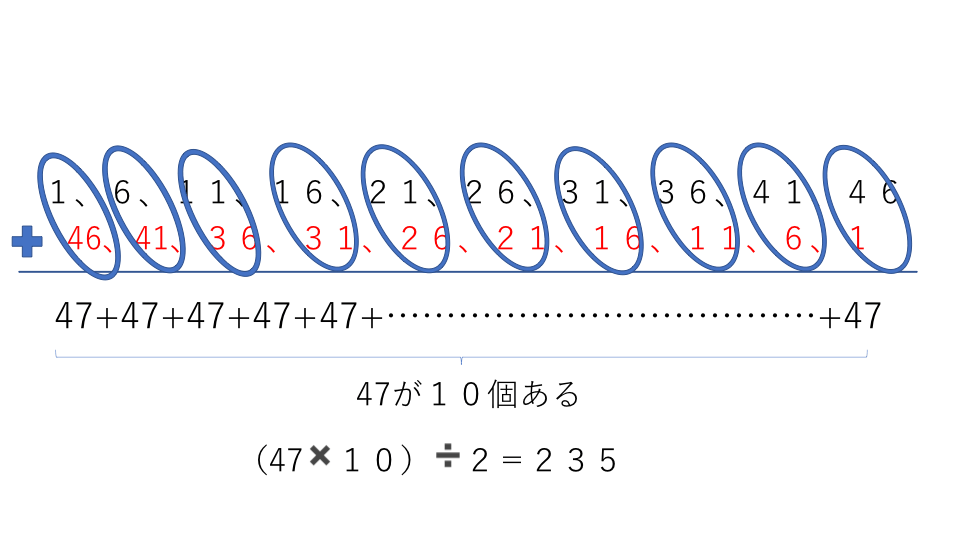
上の図のように数列を書いて、赤の字のように数列を反対から書きます。
そして1番目と10番目の数字、2番目と9番の数字とどんどん足していくと全て47になることがわかります。その47が10番目まで10個あることがわかるので、47×10＝470となります。

しかし、ここで終わってはいけません。(47×10)いうのは赤色の数字と黒色の数字を両方足したものです。

ここで求める数字は黒色の数字だけです。赤色の数字と黒色の数字は並び方が違うだけで同じ数字です。ですので、2つ分を求めるのではなく1つ分を求めるので式は(47×10)÷2＝235 となり　答え235になります。

この考え方を使って公式に表すと、

となります。この公式を使って、例題3の数列の15番までの和を求めると、
式は(1＋71)×15÷2＝540
答え540　となります。

それではこれまでの知識を確認するために、練習問題を行います。

練習問題1

次の数列の17番目の数字を求めなさい。また初項から第17項までの和を求めなさい。

2、4、6、8、10、12、14…

解説

まずは17番目の数字を求めます。
初項は2、公差は2とわかるので公式に当てはめて考えると

2＋2×(17-1)＝３４　　　答え３４

次に、初項から第17項の和を求めます。
公式に当てはめて考えると

(2＋34)×17÷2＝306　　 答え３０６

○番目の数字がわからないと、和を求めることができません。
ですで、○番目の数字を求めることと、○番までの和を求めることはセットで考える必要があります。

等比数列

等比数列とは、となり合う数の比一定となる数列(同じ数をかけていく数列)のことを言います。またそれぞれの数にかける数を公比と言います。

具体的な数列を使って説明すると

1、2、4、8、16、32… という数列があるとします。数列をみると、2倍ずつ増えていっていることがわかります。ですので、この時の公比は2となります。

これから等比数列数列を学んでいく上で、基本的なことになるので必ず覚えるようにしてください。

等比数列の和

等差数列でも和を求める問題が出題されます。等比数列の場合は等差数列のように、○番目の和を求めなさいという問題はあまり出題されません。次のような問題が出題されます。

例題4

1＋2＋4＋8＋16＋……＋128を計算しなさい。

解説

ひとつずつ計算するの難しいです。下の図を見てください。

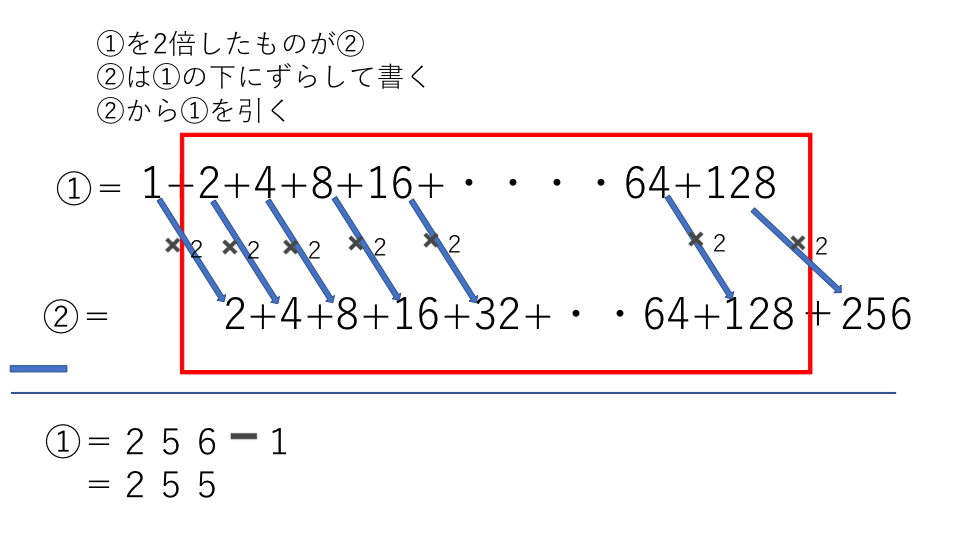
まずは等比数列であることを確認してください。2倍ずつ増えていっているので、公比が2の等比数列だとわかりました。

もともとの式を①として考えます。①の式を2倍したものを②として考えます。2倍にする理由は公差が2だからです。そして図のようにずらして②の式を書きます。②から①を引くと1と256だけが残ります。

赤い枠で囲っているところは同じ数字同士を引いているため答えが0になります。また②から①を引くと①になるのは、②は元々①を2倍した式だからです。このようにして求めると答えは255と求めることができます。

ここでのポイントは次の2つです

• 元々の式を公差倍した式を作る
• 式をずらして引く

この2つを覚えて、等比数列の問題を解きましょう。

それでは練習問題です。

練習問題2

2＋6＋18＋54＋……＋1458の計算をしなさい。

解説

まずは式が等比数列になっているか確認してください。公比が3の等比数列になっています。ですので、元の式を3倍してずらして引く方法を使います。そうすると下の図のようになります。

今回は元の式から3倍したので③とします。そうしたら、ずらして③から①を引きます。そうすると赤枠の部分は0になるので消えて、4374-2で4372が残ります。

この時、元の式を3倍しており、出てきた4372という数字は元の2倍の数になっているので、2で割ります。そうすると　答え2187　が出てきます。

練習問題3

1／2＋1／4＋1／8＋・・・＋1/64の計算をしなさい。

解説

分数になっても慌てないでください。まずはこの式が等比数列になっているのかを見ます。

公比が1／2の等比数列であることがわかります。ですので、同じように元の式に公比倍かけて、ずらして引くことをすると下の図のようになります。

元々の数字1／２倍しているので、ずらして引いた後2倍するのを忘れないようにしましょう。答え63/64

階差数列

階差数列とは、各項の差が数列のようになっている数列のことを言います。

例えば　2、3、5、8、12、… このような数列のことです。一見規則性が無いように思われますが、2から3は＋1、3から5は＋2、5から8は＋3、8から12 は＋4となっています。このように差に数列のように規則性があるものを階差数列と呼びます。

例題5

1、2、4、7、11、16…のような数列のときの10番目の数を答えなさい。

解説)

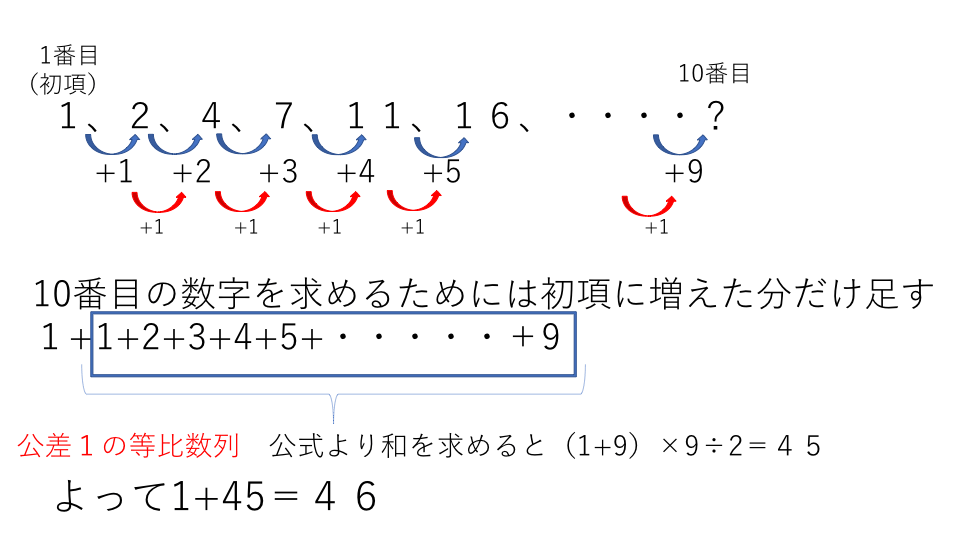
上の図を見てください。各項の差が1ずつ増えていっています。このような形は階差数列です。

10番目の前はどれだけ足されているか考えると9増えていることがわかります。なぜなら、2番目の時は1増加、3番目の時は2増加、4番目の時は3増加となっているためです。

10番目の数字を求めるためには初項に10番目まで増えた分を足せば求めることができます。そうすると式は1＋1＋2＋3＋4＋5…＋9となります。

ここで図の赤枠で示している部分に注目してください。この部分は等差数列になっています。ですので、等差数列の○番までの和の公式を使って求めることができます。

そして出てきた値に初項を足すと　1＋45＝46となります。答え４６

まとめ

いかがだったでしょうか？数列の問題パターンはいくつもあります。今回お伝えした内容を根本から理解していれば応用問題が来ても、解くことができます。難問と言われる問題も等差数列、等比数列、階差数列の組み合わせでできています。ですので、まずは今回学習した部分を完璧にして、問題をこなしていくようにしてください。

少しでも皆様のお役に立てれば幸いです。最後までご覧いただきありがとうございました。

＼ 30日で社会の偏差値がアップ！ ／
スタディアップの教材はこちら
【たった5分で丸わかり】