中学受験の算数で出題される単元「面積」。図形の性質やポイントを見抜いて、面積を求めていかなければなりません。しかし、中学受験で出題される面積の問題は、単純に公式に当てはめて考えるだけでは解けないものも多く、いくつかの図形の組み合わせに分解しなおして考え、その上で、基本的な公式を使う必要があります。
面積の単元は個別に対策を行う必要があり、ある程度の応用問題(難問)に慣れておく必要があるため、この記事では、面積の応用問題(難問)について解説していきます。面積の問題を始めて学習する人や、面積の応用問題がなかなか解けない人でも理解しやすいように解説しています。この記事を読むことで、面積の応用問題(難問)が解けるようになります。
中学受験は算数や国語ではなく、「社会」の出来で合否が決まります!
そのため、第一志望に合格したいのであれば、社会を家庭学習でまず最初に固めるのが断トツの近道です!
【社会を最初に固めるべき理由】
● 算数の1点と社会の1点は、総合点で考えれば同じ1点
● 社会は暗記教科で学習センスがいらない!
● 社会は塾任せでは絶対に伸びない、家庭学習で伸ばす!
【短期間で社会の偏差値を上げたい方必見!】
短期間で偏差値を10以上アップさせた受験生多数!社会の偏差値を最速でアップできる社会に特化したスーパー教材を下記のページでご紹介しています!
\ 30日で社会の偏差値がアップ! /
スタディアップの教材はこちら
【たった5分で丸わかり】
面積① 基本事項
応用問題を解く前に、以下の公式は必ず覚えてください。
- 正方形の面積=1辺×1辺
- 長方形の面積=たて×横
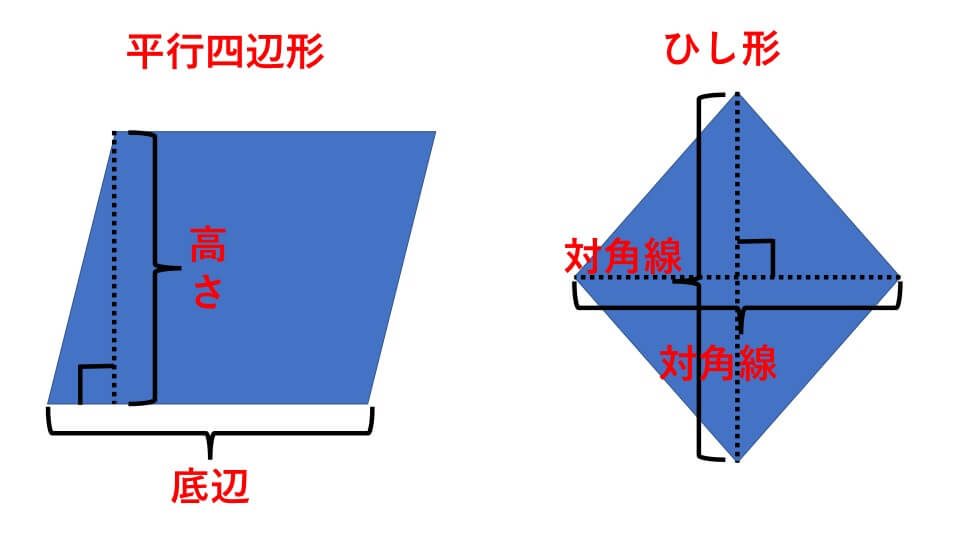
- 平行四辺形の面積=底辺×高さ
- ひし形の面積=対角線×対角線÷2
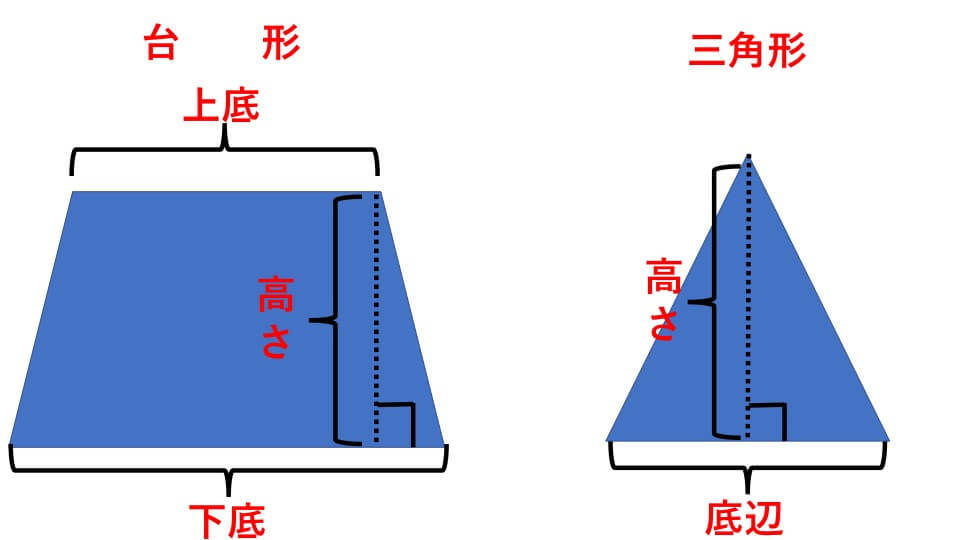
- 台形の面積=(上底+下底)×高さ÷2
- 三角形の面積=底辺×高さ÷2
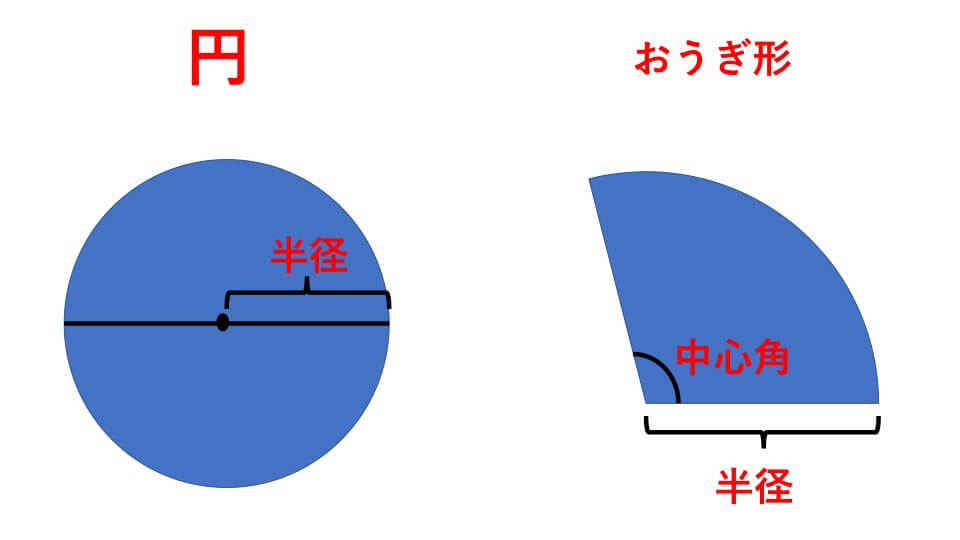
- 円の面積=半径×半径×円周率(3.14)
- おうぎ形の面積=半径×半径×円周率×中心角/360°
公式の成り立ちから知りたい人や公式がまだ曖昧な人は、下記の平面図形の記事を読んでから、これから解説する問題に取り組んでください。

面積② 複雑な図形の面積
例題1
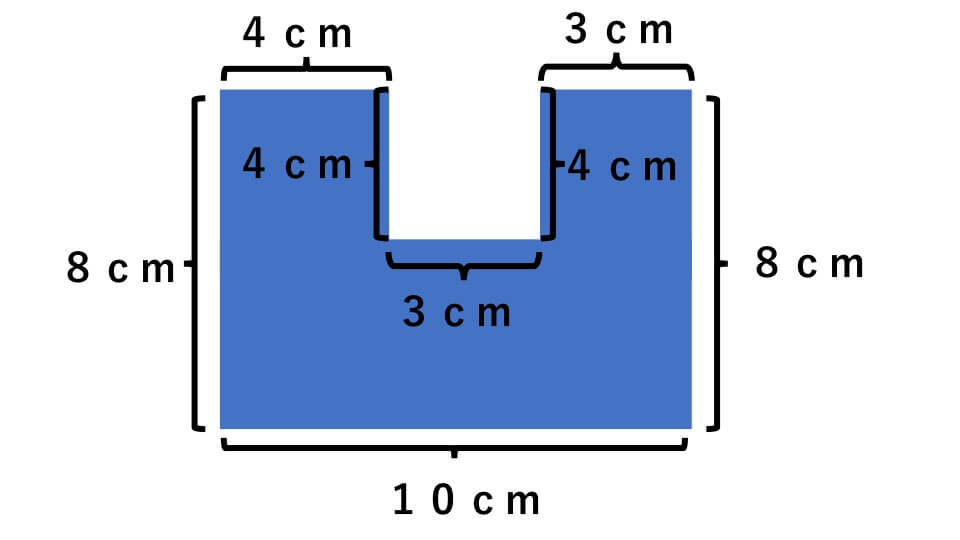
次の図形の面積を求めなさい。
解説
全体の面積を考えてから、一部の面積を取り除いて考えていきます。下の図をみてください。

図のように赤線の補助線を入れて考えると、全体の長方形から凹んだ部分の長方形を引けば求められそうです。全体の長方形の面積は、
8×10=80㎠
凹んだ部分の長方形の面積は、
4×3=12㎠
全体の長方形から凹んだ部分の長方形を引くので、
80㎠-12㎠=68㎠
よって、答え 68㎠
別解
下の図のように補助線を入れることでも求めることができます。
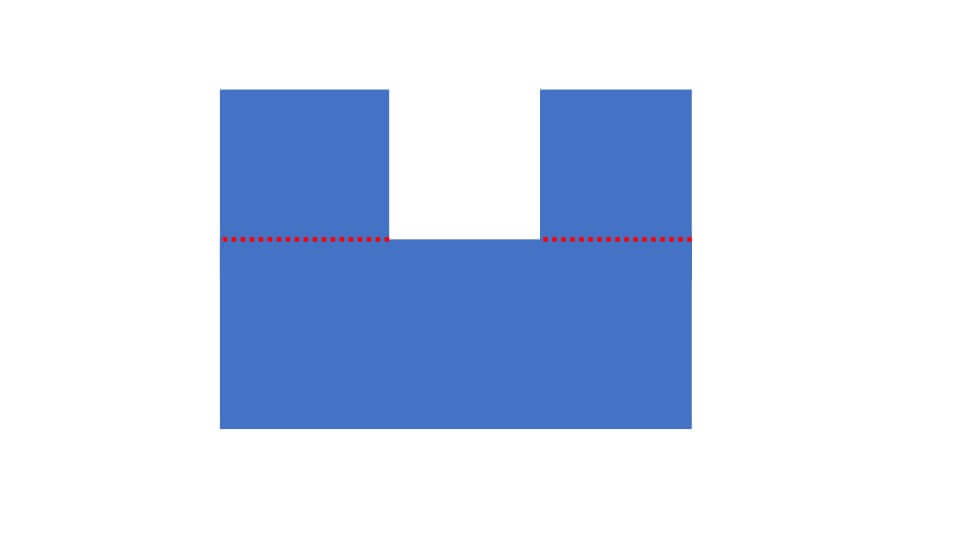
このように3つの長方形に分けることができます。それぞれの長方形を求めて、全て足せば面積を求めることができるので、式は、
4×4+4×3+(8-4)×10=68
よって、答え 68㎠
例題2
下の図をように、長方形の中に、たてと横に幅2cmの隙間を作りました。このときの面積を求めなさい。
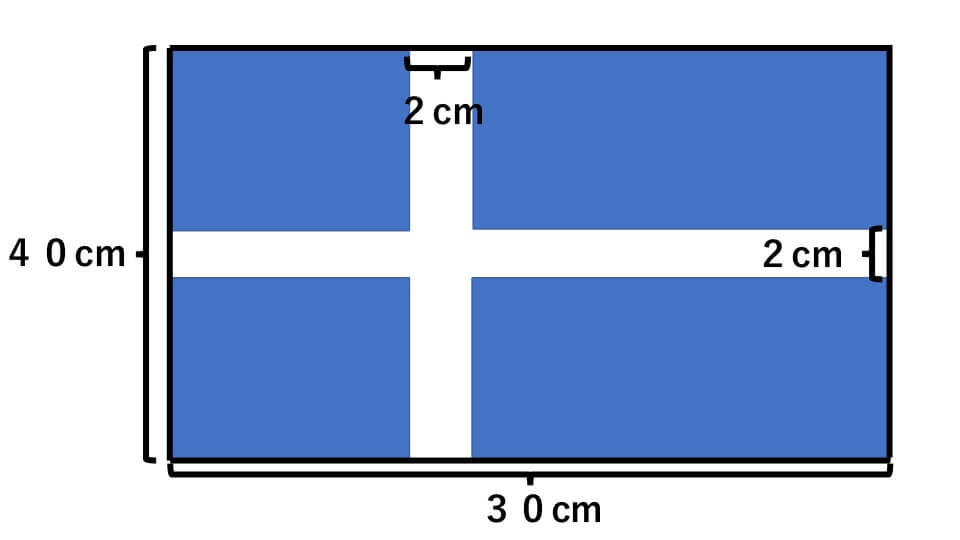
解説
隙間の部分を端に移したと考えると、下の図のようになります。
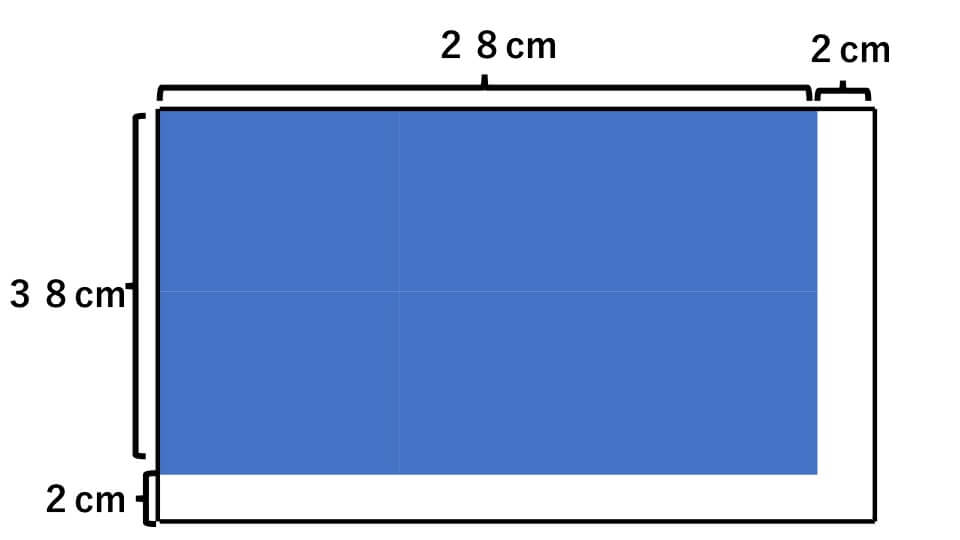
すると図形は、たて(40-2)cm、横(30-2)cmの長方形になるので、面積は、
(40-2)×(30-2)=1064
よって、答え 1064㎠
面積③ 円が絡んだ複雑な図形
例題3
下の図の色の付いた部分の面積を求めなさい。ただし円周率は3.14する。
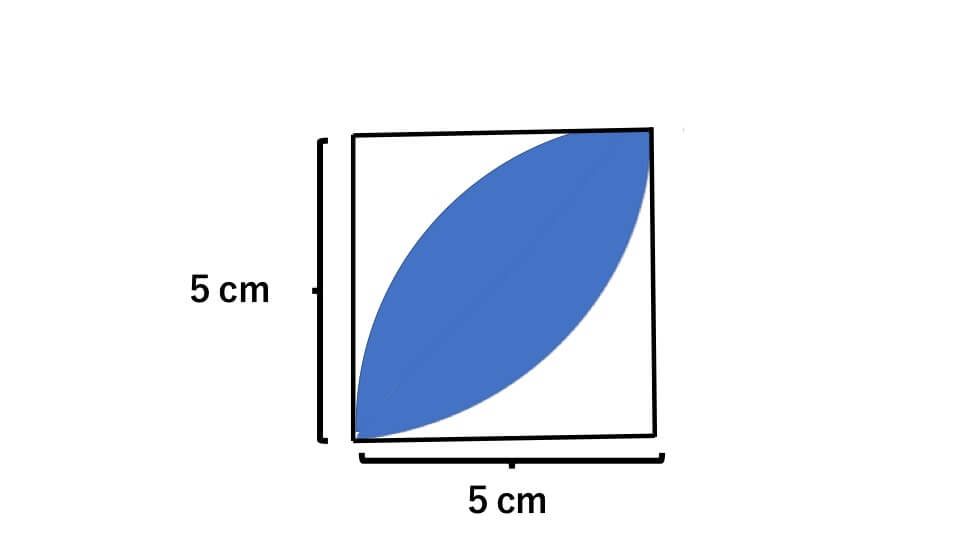
解説
下の図のように図形を分けて、考えます。
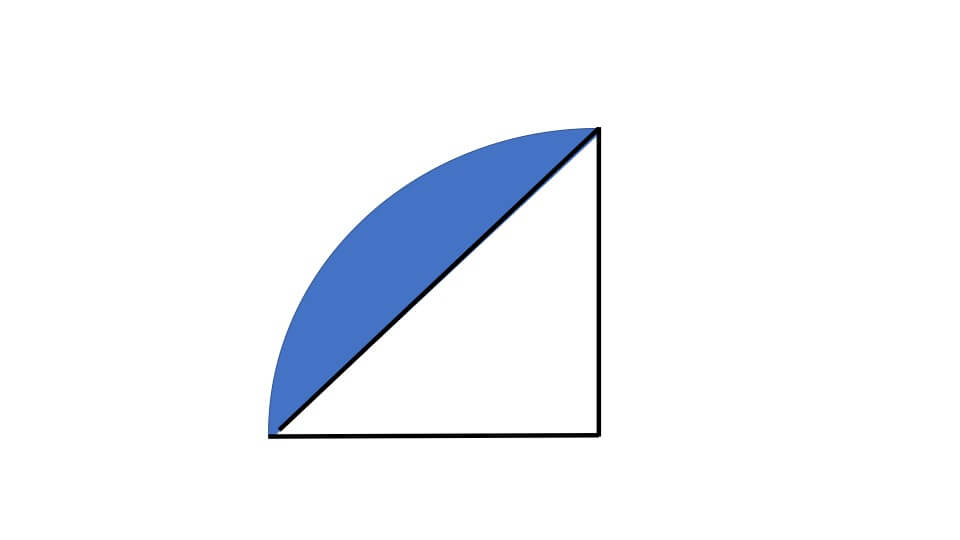
分けた後の図形の色の付いた部分は4分の1の円の面積(中心角90°のおうぎ形)から直角二等辺三角形の面積を引けば求めることができます。
4分の1の円の面積は半径が5cmなので、
5×5×3.14×1/4=19.625㎠
直角二等辺三角形の底辺は5cm、高さは5cmなので、
5×5×÷2=12.5㎠
よって、分けた後の図形の色の付いた部分の面積は、
19.625-12.5=7.125㎠
この図形が二つあるので、
7.125×2=14.25㎠
よって、答え 14.25㎠
例題4
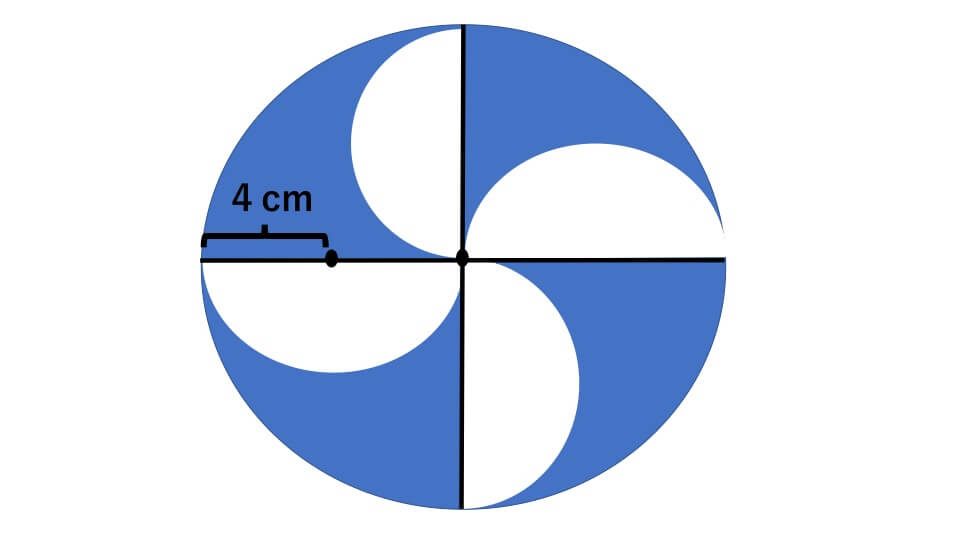
下の図の色の付いた部分の面積を求めなさい。ただし円周率は3.14する。
解説
面積は、大きい円の面積と、大きい円の中にある半円の面積4つ分の差で求めることができます。
大きい円の半径は8cm(4+4)なので面積は、
8×8×3.14=200.96㎠
半円の半径は4cmなので面積は、
4×4×3.14×1/2=25.12㎠
この半円が4つあるので、
25.12×4=100.48㎠
大きい円の面積と、大きい円の中にある半円の面積4つ分の差は、
200.96-100.48=100.48㎠
よって、答え 100.48㎠
面積④ 重なりや移動でできた面積
例題5
長方形と正方形が下の図のように重なっています。色の付いた部分の面積を求めなさい。
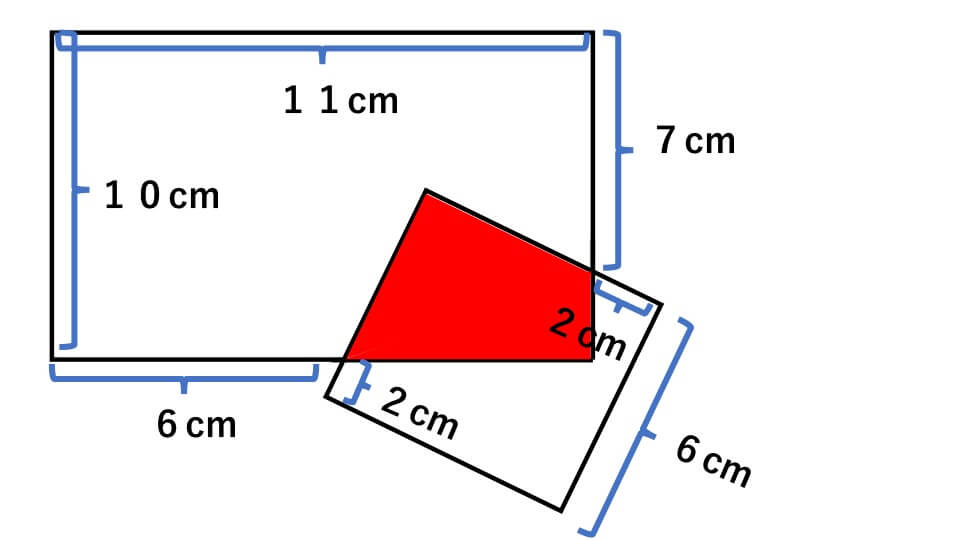
解説
重なった部分の四角形をABCDとして補助線を入れると、下の図のようになる。
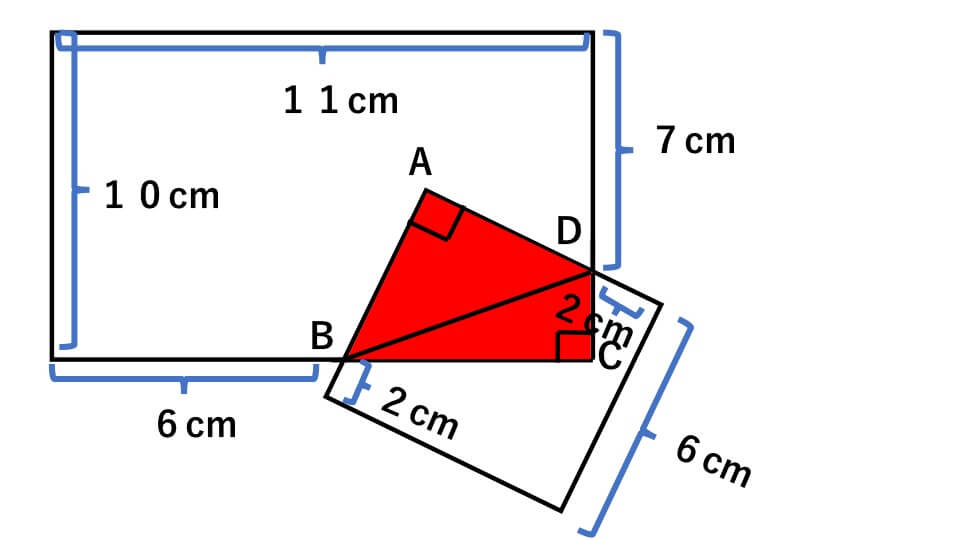
四角形ABCDの面積は、2つの三角形の面積を求めて足せば求めることができる。
辺ABの長さは、6-2=4cm
辺ADの長さは、6-2=4cm
よって三角形ABDの面積は、
4×4÷2=8㎠
辺BCの長さは、11-6=5cm
辺CDの長さは、10-7=3cm
よって三角形BCDの面積は、
5×3÷2=7.5㎠
四角形ABCDの面積は
8+7.5=15.5㎠
よって、答え 15.5㎠
例題6
下の図のような台形ABCDがあります。点Pは、頂点Aより出発して台形ABCDの辺上を秒速2cmの速さで、頂点B、頂点C、を通って頂点Dまで進みます。11秒後の四角形ABCPの面積を求めなさい。
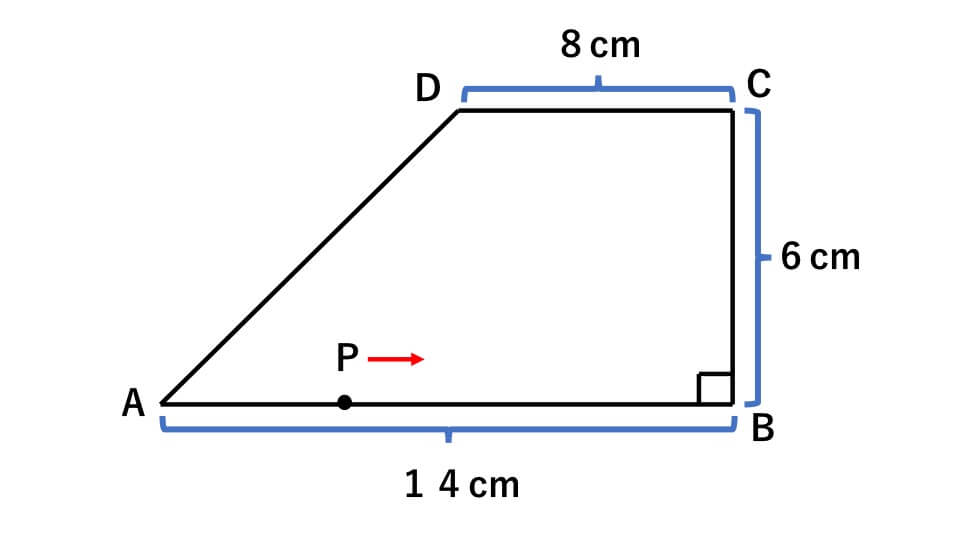
解説
秒速2cmの速さで、11秒間進むと以下のような図形になります。
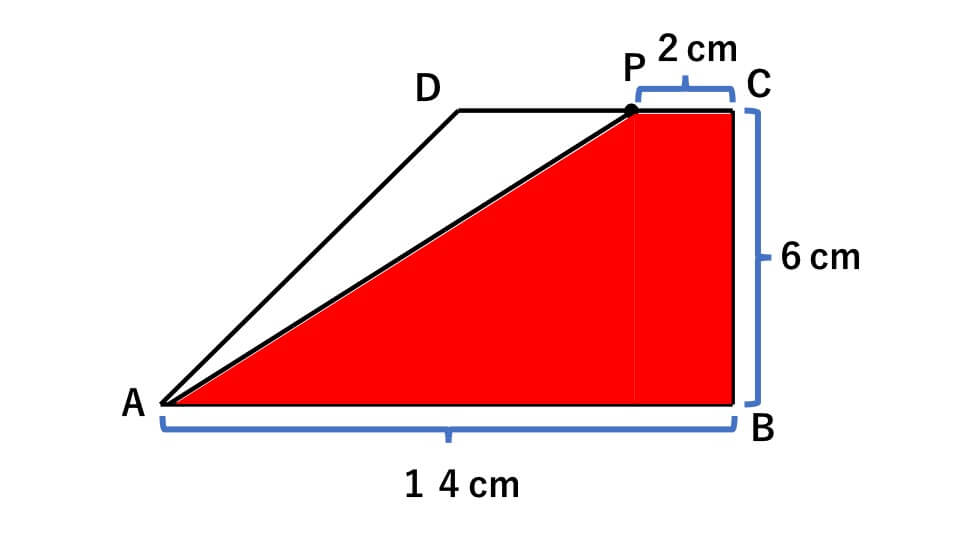
上底2cm、下底14cm、高さ6cmの台形になるので、面積は、
(2+14)×6÷2=48㎠
よって、答え48㎠
まとめ
いかがだったでしょうか?面積の応用問題は、補助線を入れてどんな図形の組み合わせでできているのか考えて公式を使うことが大切だとわかってもらえたと思います。
面積の問題は無数にあるので、お手持ちの問題集で様々な問題に触れて、慣れていってください。
最後までご覧いただきありがとうございました。
中学受験は算数や国語ではなく、「社会」の出来で合否が決まります!
そのため、第一志望に合格したいのであれば、社会を家庭学習でまず最初に固めるのが断トツの近道です!
【社会を最初に固めるべき理由】
● 算数の1点と社会の1点は、総合点で考えれば同じ1点
● 社会は暗記教科で学習センスがいらない!
● 社会は塾任せでは絶対に伸びない、家庭学習で伸ばす!
【短期間で社会の偏差値を上げたい方必見!】
短期間で偏差値を10以上アップさせた受験生多数!社会の偏差値を最速でアップできる社会に特化したスーパー教材を下記のページでご紹介しています!
\ 30日で社会の偏差値がアップ! /
スタディアップの教材はこちら
【たった5分で丸わかり】

