中学受験の算数で出題される単元「角度」。図形の性質や直線と交わりの関係を使って、各角度を求めていきます。角度の問題では図形と角の性質を覚えなければ、簡単に解くことができない問題が非常に多い分野です。
小学生の間に図形と角の性質を覚え、角度の問題に対して苦手意識がなくならないと、中学、高校と苦手を引きずることになります。そのため小学生の間にしっかりと基礎を固めておく必要があります。
- 算数が苦手な人
- 角度の問題を初めて学習する人
- 角度の問題が苦手な人
このような人たちでも理解しやすいように、基礎からわかりやすく解説しています。この記事を読むことで、角度の基礎から理解でき、角度の問題に対して苦手意識がなくなります。
中学受験は算数や国語ではなく、「社会」の出来で合否が決まります!
そのため、第一志望に合格したいのであれば、社会を家庭学習でまず最初に固めるのが断トツの近道です!
【社会を最初に固めるべき理由】
● 算数の1点と社会の1点は、総合点で考えれば同じ1点
● 社会は暗記教科で学習センスがいらない!
● 社会は塾任せでは絶対に伸びない、家庭学習で伸ばす!
【短期間で社会の偏差値を上げたい方必見!】
短期間で偏差値を10以上アップさせた受験生多数!社会の偏差値を最速でアップできる社会に特化したスーパー教材を下記のページでご紹介しています!
\ 30日で社会の偏差値がアップ! /
スタディアップの教材はこちら
【たった5分で丸わかり】
角度① 基本事項
直線と角度の関係
まず始めに覚えてもらいたい角が3つあります。1つ目は対頂角です。下の図をみてください。
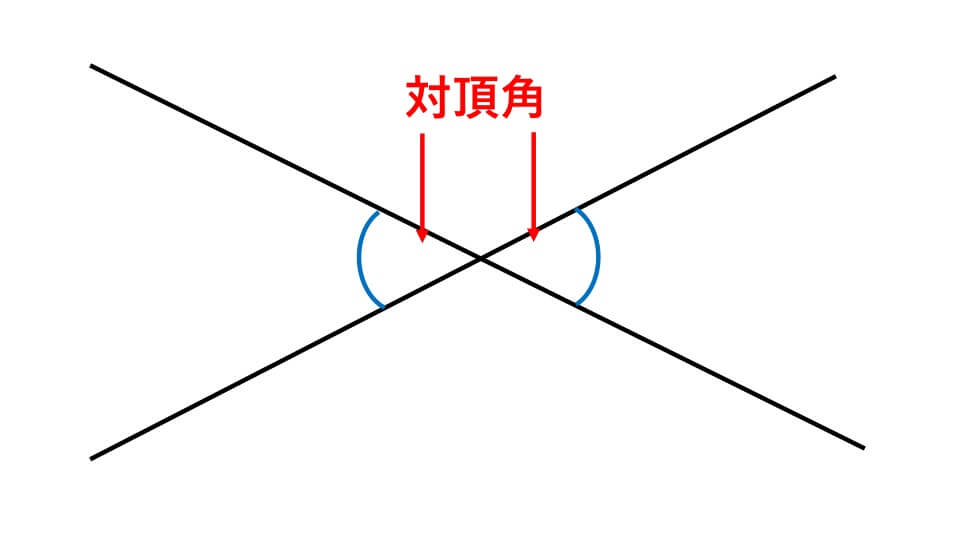
対頂角とは、上の図のように2つの直線が交わってできる、向かい合った角のことを言います。
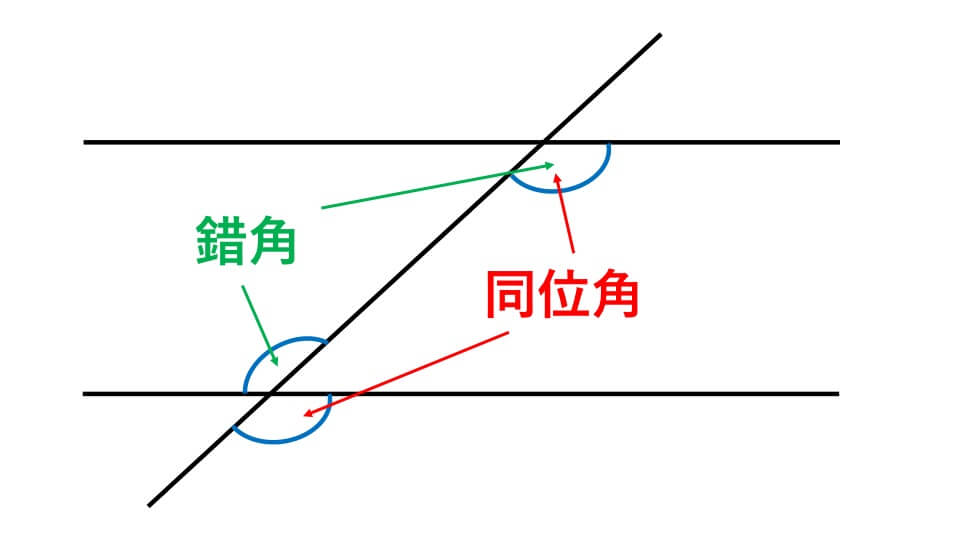
2つ目は同位角です。同位角とは、上の図のように2つの直線に1つの直線が交わってできる角のうち、同じ側にあって、向きも角度も同じ角のことを言います。
3つ目は錯角です。錯角とは、上の図のように2つの直線に1つの直線が交わってできる角のうち、反対側にあって、向きも反対の角のことを言います。
同位角と錯角は混合しやすいので、ここで違いをはっきりさせて覚えてください。
- 対頂角は等しい
- 平行な直線に1つの直線が交わるとき、同位角は等しく、錯角も等しくなる
三角形の角の性質
皆さんが普段使っている三角定規の3つの角度は、(90°、45°、45°)と(90°、30°、60°)になっています。
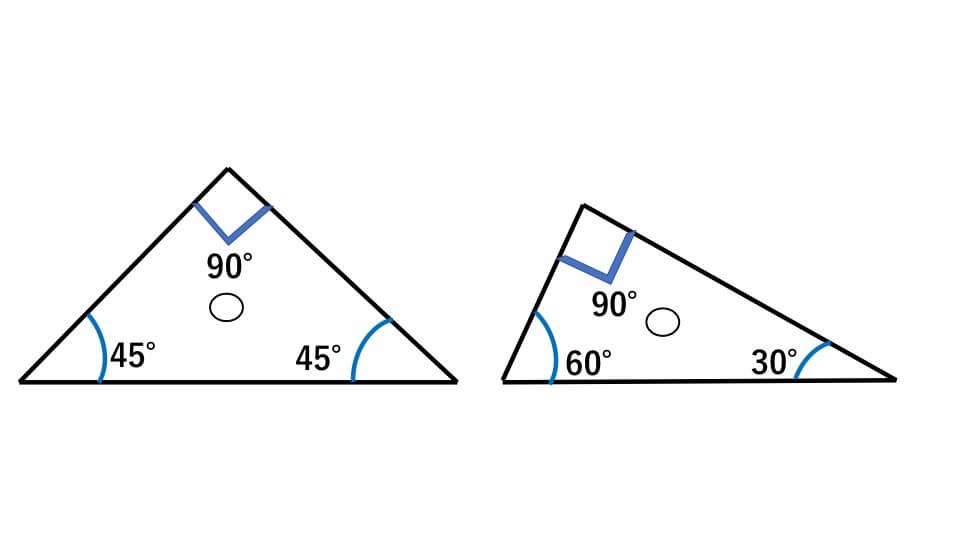
このことを知らない人は意外と多いのではないでしょうか。問題として出題されるときは、知っている前提で聞かれるので必ず覚えてください。
図形の内側の角を内角、図形の1辺と、その隣り合った辺を伸ばした直線とでできる角を外角と言います。
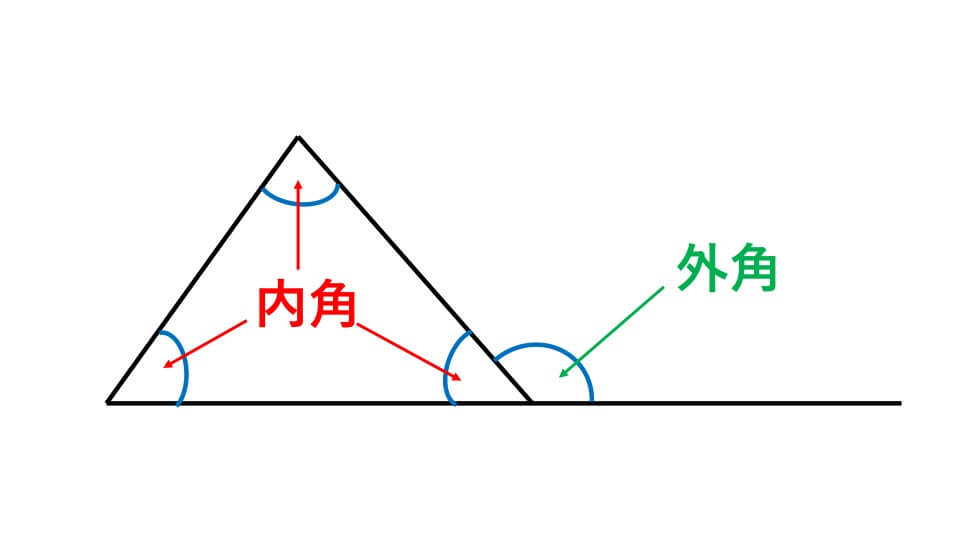
すでにご存知のことだと思いますが、三角形の内角の和は180°になります。また外角の和は何角形になろうとも360°です。必ず覚えてください。
- 三角形の内角の和=180°
- 多角形は何角形でも外角の和=360°
多角形の性質
全ての多角形は、辺の数から2引いた数の三角形に分けることができます。この性質を利用すれば、多角形の内角の和を求めることができます。
例えば、下の図のような五角形があったとします。
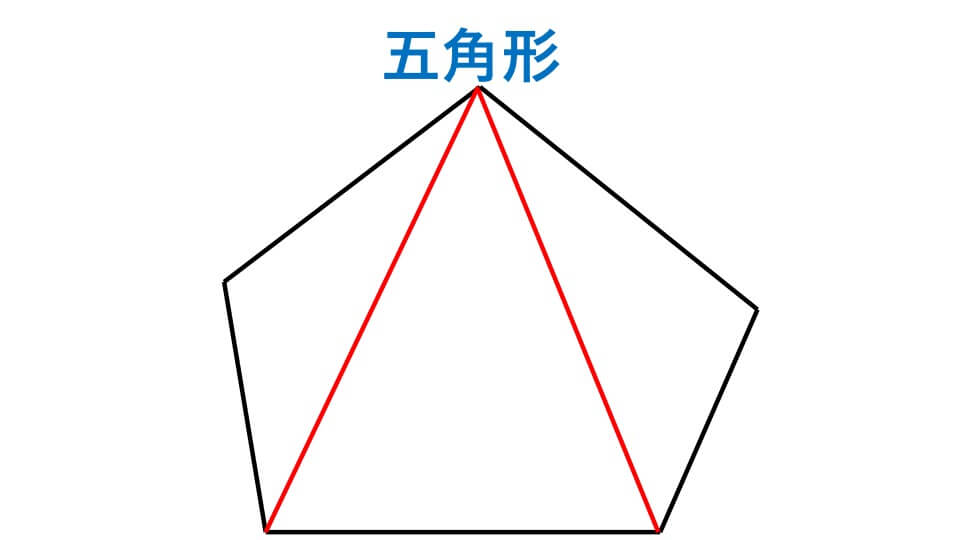
この五角形は赤線で示したように三角形3つ分に分けることができます。三角形の数は(5-2=3)で求めることができます。
三角形の内角の和は180°なので、五角形の内角の和は、180°×3=540° になります。
多角形の角の性質を下の表にまとめました。必ず覚えてください。この表を理解することで、どんな多角形が来ても内角の和を求めることができます。
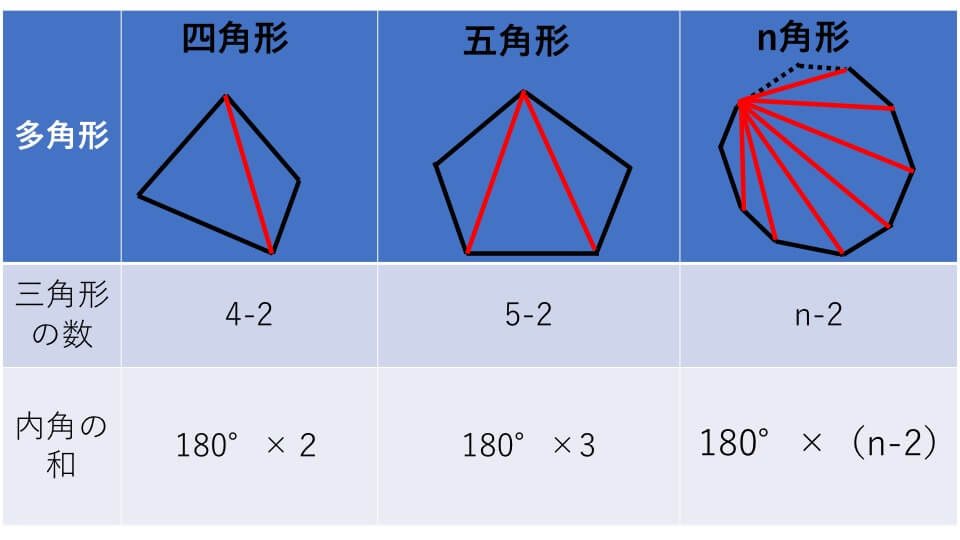
n角形の内角の和=180°×(n-2)
角度② 基本問題
例題1
下の図のように、2本の直線が交わっています。A、B、Cの角の大きさは、それぞれ何度になるか求めなさい。
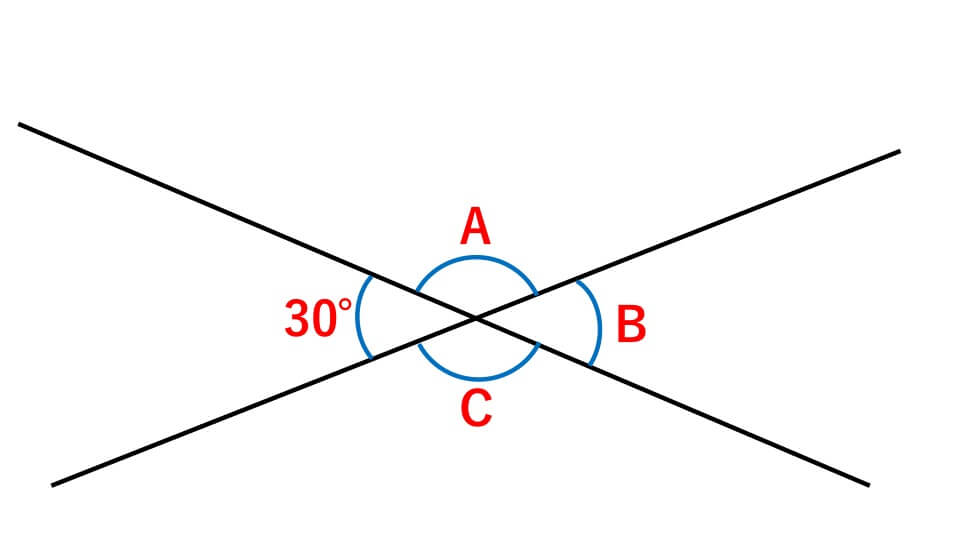
解説
まずBの角度から求めていきます。向かい合った角、つまり対頂角は等しいので、B=30°
次にAの角度を求めます。直線の角の大きさは180°です。そのためAの角度は、180°-30°=150°
Cの角度は対頂角よりAと等しいので、C=150°
よって、答え A=150°、B=30°、C=150°
例題2
下の図で、直線アとイ、直線ウとエはそれぞれ平行です。このときのA、B、Cの角の大きさは、それぞれ何度になるか求めなさい。
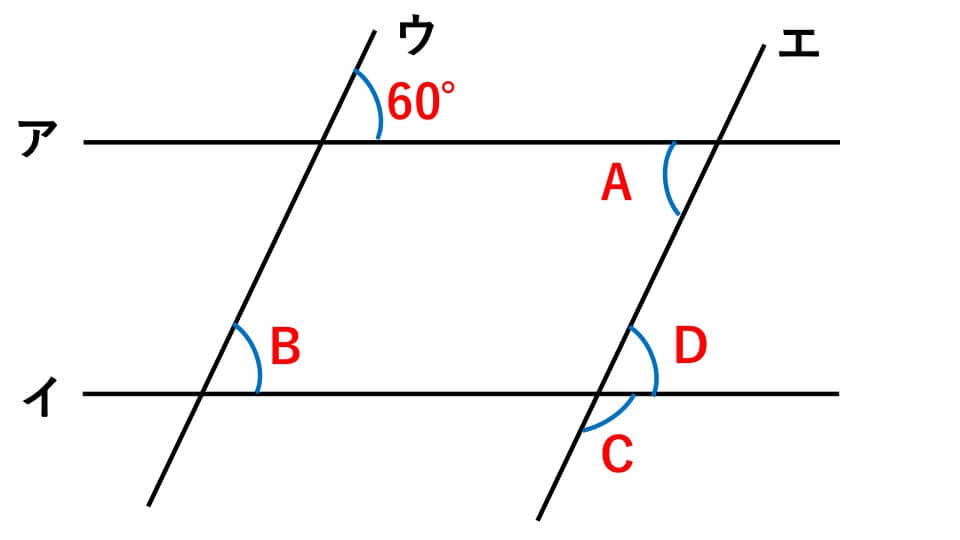
解説
平行な直線に1つの直線が交わる問題は、同位角は等しく、錯角も等しくなるという性質を使って解きます。
Aは直線アとウの交わる角(60°)と平行線の錯覚になるので、A=60°
Bは直線アとウの交わる角(60°)と平行線の同位角になるので、B=60°
Cはいきなり求めることができないので、Dの角度を求めてから考えます。DはBと同位角の関係になるので、
D=60°
直線の角の大きさは180°です。そのためCの角度は、180°-60°=120°
よって、答え A=60°、B=60°、C=120°
例題3
下の四角形のAの角度を求めなさい。
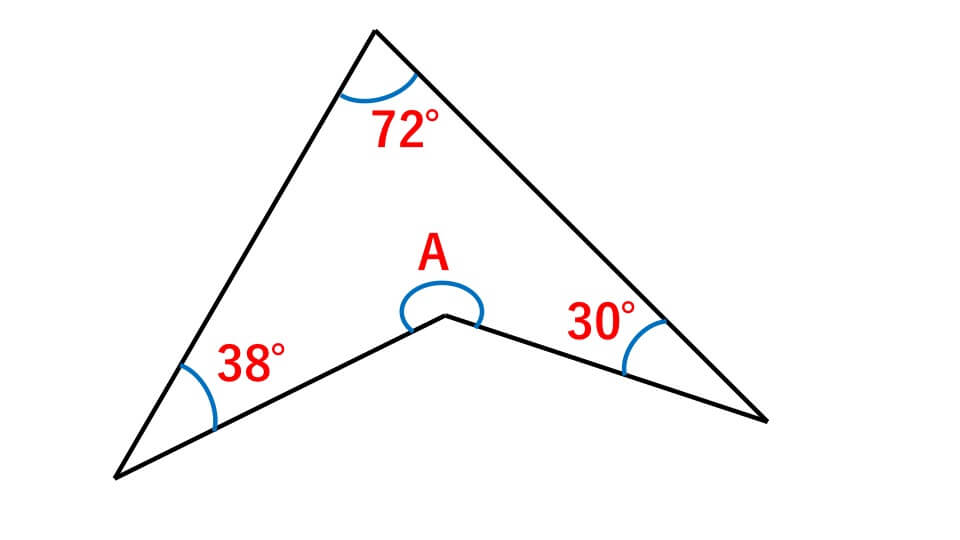
解説
下の図のように四角形の1本の対角線で2つの三角形に分けます。
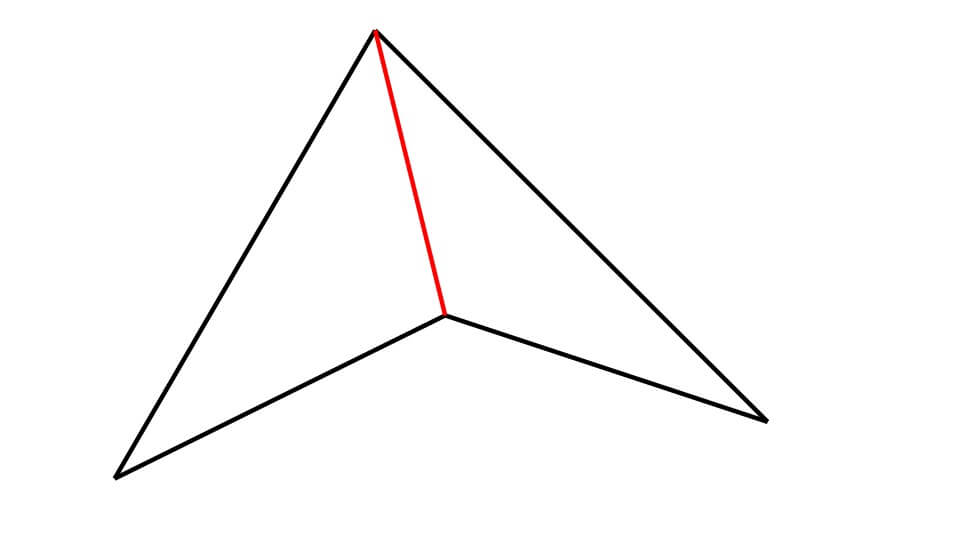
三角形の内角の和は180°なので、この四角形の内角の和は180°×2=360°になります。
ですのでAの角度は、360°-(72°+38°+30°)=220°
よって、答え A=220°
角度③ 応用問題
例題4
1組の三角定規を下の図のように重ねました。この図でAの角度は何度になるか求めなさい。
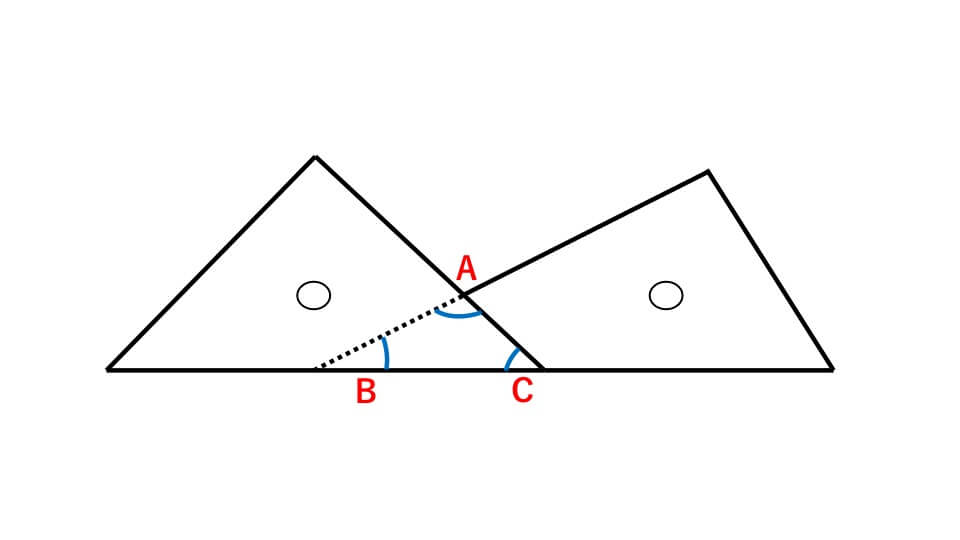
解説
基本事項でもお伝えしたように三角定規は下の図のように角度が決まっています。

問題の図でBは30°、Cは45°なので、三角形の内角は180°である性質を利用すると、Aの角度は、
180°-(30°+45°)=105°
よって、答え A=105°
例題5
下の図は長方形の紙を点線にそって折り曲げたものです。①は30°になりました。②と③の角度は何度になるか求めなさい。
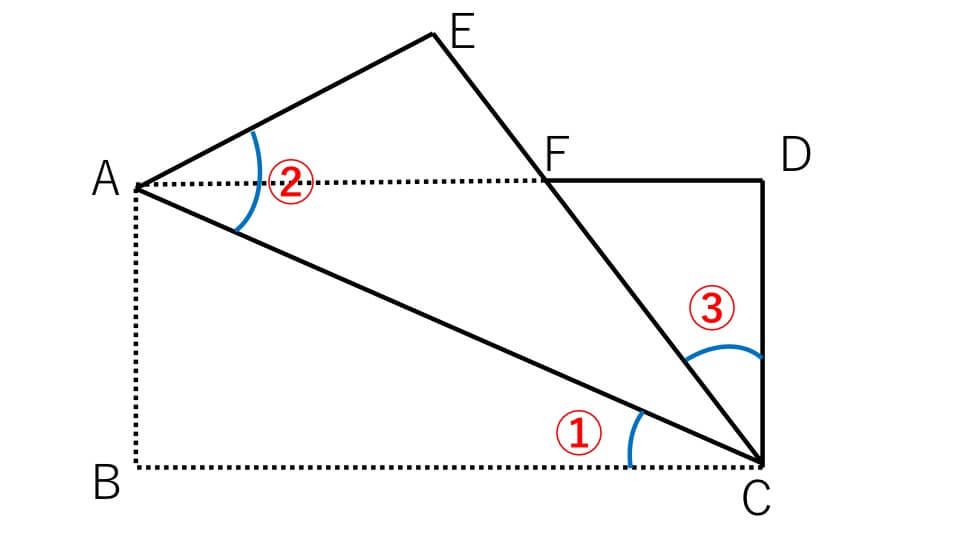
解説
②の角度は角BACと等しくなる(角BACは折り曲げる前の②の角と同じだから)ので、②の角度は、
180°-(90°+①)=180°-(90°+30°)=60°
①の角度と角ACEは等しい(角ACEは折り曲げる前の①の角と同じだから)ので、③の角度は90°から①と角ACEを足した角度を引けば求めることができる。ですので、③の角度は、
90°-(30°+30°)=30°
よって、答え ②=60°、③=30°
例題6
下の図のような星型の図形があります。星の中にある五角形は正五角形です。このときの①の角度は何度になるか求めなさい。

解説
まず初めに、正五角形の1つの内角の大きさを求めます。正五角形の内角の和は、
180°×(5-2)=540°
正五角形なので一つひとつの内角は等しいでの、
540÷5=108°
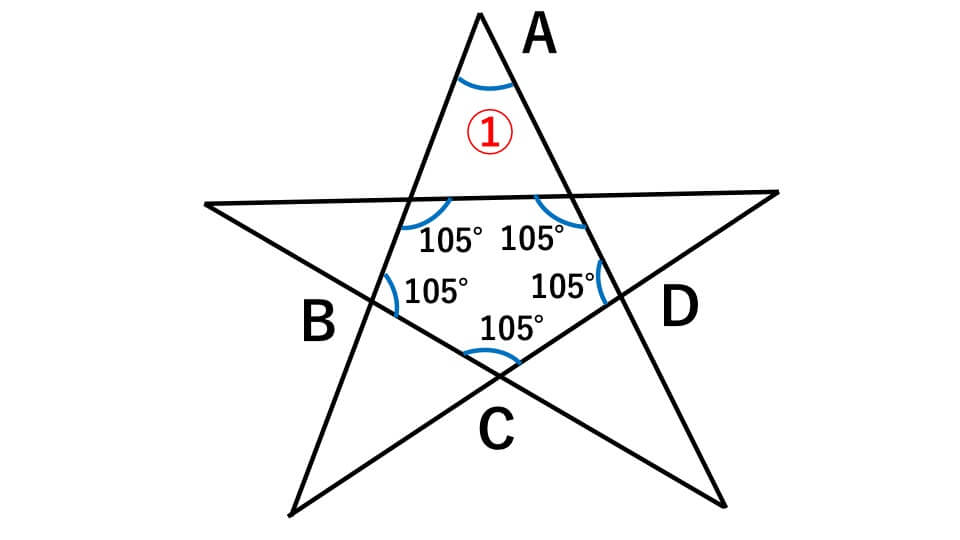
上の図の四角形ABCDで、①+108×3=360°になるので(四角形の内角の和は180°×(4-2)=360°だから)、①の角度は、
360°-108×3=36°
よって、答え ①=36°
まとめ
いかがだったでしょうか?
どんなに難しい角度の問題も基本事項をしっかりと覚えることで答えが導き出せることがわかってもらえたと思います。
角度の問題は今回お伝えした基本事項が組み合わさってできています。角度の問題を何度も解いて基本事項をしっかりと覚えましょう。
中学受験は算数や国語ではなく、「社会」の出来で合否が決まります!
そのため、第一志望に合格したいのであれば、社会を家庭学習でまず最初に固めるのが断トツの近道です!
【社会を最初に固めるべき理由】
● 算数の1点と社会の1点は、総合点で考えれば同じ1点
● 社会は暗記教科で学習センスがいらない!
● 社会は塾任せでは絶対に伸びない、家庭学習で伸ばす!
【短期間で社会の偏差値を上げたい方必見!】
短期間で偏差値を10以上アップさせた受験生多数!社会の偏差値を最速でアップできる社会に特化したスーパー教材を下記のページでご紹介しています!
\ 30日で社会の偏差値がアップ! /
スタディアップの教材はこちら
【たった5分で丸わかり】
次は面積のポイント解説です。


