この記事では、中学受験の算数で出題される速さ、割合、食塩水、図形の問題を掲載しています。それぞれ詳しい解説付きなので、わからない問題も解説を読むことで正しく理解できるようになっています。
- 中学受験の算数の問題を多く解きたい人
- 中学受験の算数が苦手な人
- 算数を出題されやすい分野別で学習したい人
このような受験生はこの記事で紹介している問題を解いて、算数の得点アップを目指していきましょう。
中学受験は算数や国語ではなく、「社会」の出来で合否が決まります!
そのため、第一志望に合格したいのであれば、社会を家庭学習でまず最初に固めるのが断トツの近道です!
【社会を最初に固めるべき理由】
● 算数の1点と社会の1点は、総合点で考えれば同じ1点
● 社会は暗記教科で学習センスがいらない!
● 社会は塾任せでは絶対に伸びない、家庭学習で伸ばす!
【短期間で社会の偏差値を上げたい方必見!】
短期間で偏差値を10以上アップさせた受験生多数!社会の偏差値を最速でアップできる社会に特化したスーパー教材を下記のページでご紹介しています!
\ 30日で社会の偏差値がアップ! /
スタディアップの教材はこちら
【たった5分で丸わかり】
中学受験 算数の無料問題~速さ~
問1
分速300mの速さの自転車で17分走ったとき、何km進むか求めなさい。
解説
速さの問題では以下の公式を利用します。
- 速さ=道のり÷時間
- 道のり=速さ×時間
- 時間=道のり÷速さ
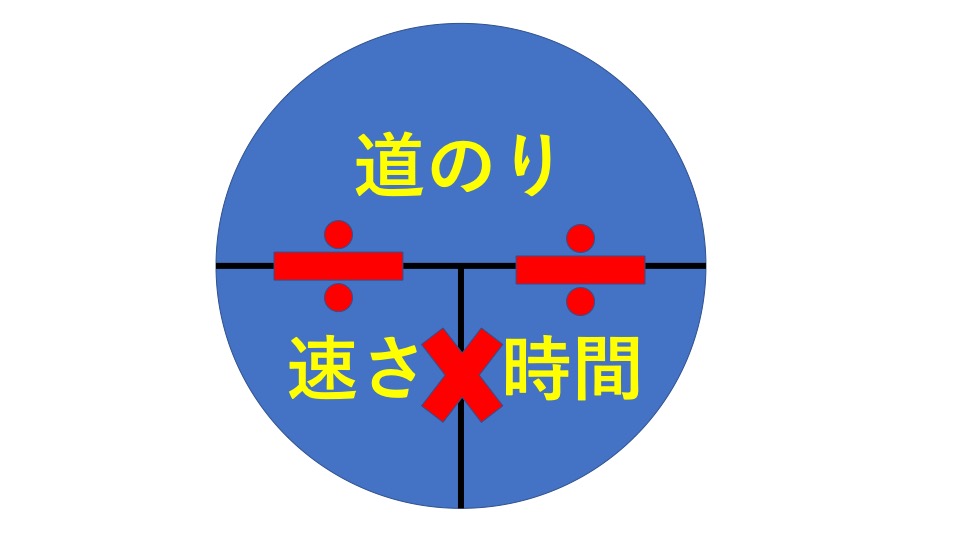
この問題では道のりを求めるので、公式より、
300×17=5100(m)
求めた値の単位はmなのでkmに直すと
答え 5.1km
問2
11.2kmの道のりを7分で走る乗り物があります。この乗り物の速さは分速何kmか求めなさい。
解説
この問題では求めるものは速さなので、公式より式は、
11.2÷7=1.6(km)
よって 答え 1.6km
問3
太郎くんは自動車で78kmの道のりを往復しました。行きは5時間、帰りは8時間かかりました。このときの平均の速さを求めなさい。
解説
往復の道のりを求めて、それを往復の時間で割ることで、往復の平均の速さを求めることができます。
往復の道のりは 78×2=156(km)
往復の時間は 5+8=13(時間)
つまり156kmの道のりを13時間かけて移動したことになるので、平均の速さは、
156÷13=12(km)
よって 答え 時速12km
問4
長さが200mで秒速30mで走る赤色の電車と長さが100mで秒速20mで走る青色の電車があります。2つの電車は向かい合って走っています。赤色の電車と青色の電車の先頭が出会ってから、完全にすれ違うまでに何秒かかりますか?
解説
赤色の電車の先頭に乗っている人の視点で考えていきます。完全にすれ違うときに電車が進む距離は2つの電車の長さの和に等しいので、
200+100=300(m)
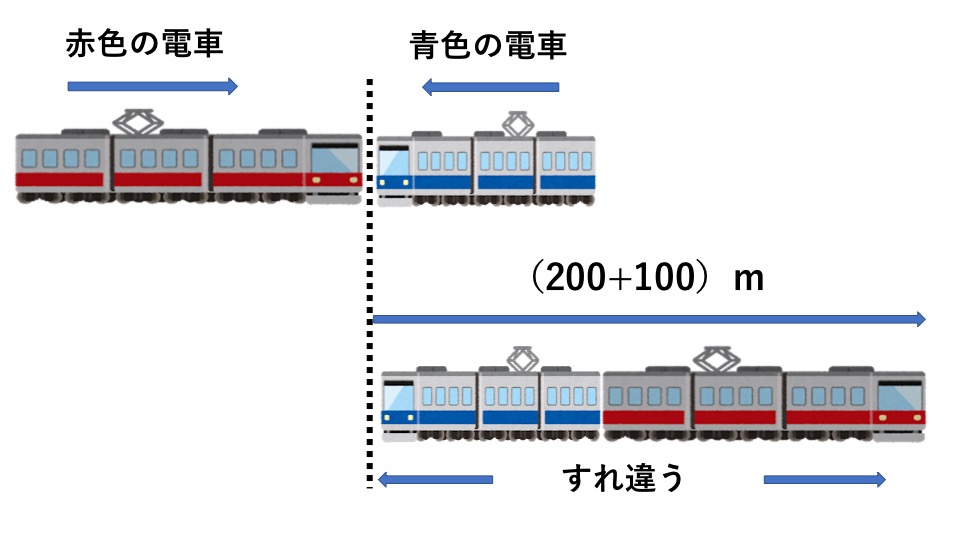
このとき、赤色の電車に乗っている人の視点では、赤色の進む速さは2つの電車の速さの和に見えるので、その進む速さは、
30+20=(秒速)50(m)
よって、完全にすれ違うのにかかる時間は、
300÷50=6(秒)
答え 6秒
中学受験 算数の無料問題~割合~
問1
花子さんの体重は32.5kgで、お父さんの体重は58.5kgです。お父さんの体重は花子さんの体重の何倍か求めなさい。
解説
割合の公式では以下の3つがあります。
- 割合=比べる量÷もとにする量
- 比べる量=もとにする量×割合
- もとにする量=比べる量÷割合
この問題では比べる量ともとにする量がそれぞれわかっています。「比べる量」はお父さんの体重、「もとにする量」は花子さんの体重、これらを公式に当てはめて計算すると、
58.5÷32.5=1.8
よって 答え 1.8倍
問2
花子さんのクラスで携帯を持っている人は16人います。これはクラス全体の1/3に当たります。このクラスは全員で何人いるか求めなさい。
解説
この問題では「比べる量」が携帯を持っている人の人数、「もとにする量」がクラス全員の人数になっています。求める値は「もとにする量」なので、公式に当てはめて計算すると、
16÷1/3=48(人)
よって 答え 48人
問3
花子さんの学校で歯科検診が行われました。その結果虫歯がない人は全体の2/5でした。学校全体の人数は760人です。このとき、虫歯がある人は何人いるか求めなさい。
解説
虫歯がない人が全体の2/5なので、全体を1として考えたときに、虫歯がある人の割合は、
1-2/5=3/5 となります。
「もとにする量」が学校全体の人数、「比べる量」が虫歯がない人の人数なので、公式に当てはめて計算すると、
760×3/5=456(人)
よって 答え 456人
問4
太郎くんがある本を読みました。1日目は全体の2/5を読み、2日目は残りの2/7を読んだら、残りのページが36ページになりました。この本は全部で何ページあるのか求めなさい。
解説
全体を1として考えます。すると本の残り36ページの割合は(1-2/5)×(1-2/7)となります。「もとにする量」は本の全部のページになります。
全体を1とすると残り36ページの割合は、
(1-2/5)×(1-2/7)=3/7
この本のページ数は、
36÷3/7=84(ページ)
よって 答え 84ページ
中学受験 算数の無料問題~食塩水~
問1
450gの水に50gの食塩を混ぜると、何%の食塩水になるか求めなさい。
解説
食塩水の問題では以下の公式を使います。
食塩水の濃度(%)=食塩の重さ÷食塩数の重さ×100
食塩数の重さは、食塩の重さと水の重さの和になります。
この問題の全体の重さは、
450+50=500(g) になります。公式に当てはめて濃度を計算すると、
50÷500×100=10(%)
よって 答え 10%
問2
5%の食塩水200gと12%の食塩水300gを混ぜ合わせると、何%の食塩数ができるか求めなさい。
解説
混ぜ合わせた食塩水の重さは、
200+300=500(g) となります。
この食塩水に含まれる食塩の重さは5%と12%のそれぞれの食塩水の中に含まれる食塩の重さの和になります。
5%の食塩水200gに含まれる食塩の重さは、
200×0.05=10g
12%の食塩水300g に含まれる食塩の重さは、
300×0.12=36g
ですので、混ぜ合わせた食塩水に含まれる食塩の重さは、
10+36=46(g)
つまり、46gの食塩が溶けている 500gの食塩水の濃度を求めればいいので、公式に当てはめて計算すると、
46÷500×100=9.2(%)
よって 答え 9.2%
問3
10%の食塩水500gに食塩水を200g入れると、12%の食塩水ができました。このとき何%の食塩水を入れたことになるのか求めなさい。
解説
10%の食塩水に含まれる食塩の重さは、
500×0.1=50g
12 %の食塩水の重さは、
500+200=700(g) なので、12 %の食塩水に含まれる食塩の重さは、
700×0.12=84g
つまり、食塩水200gに含まれる食塩の重さは、
84-50=34(g)
よって食塩水200gの濃度は、
34÷200×100=17(%)
よって 答え 17%
問4
10%の食塩水180gから水を何gか蒸発させ、その後、食塩を10g加えたところ、食塩水の濃度は20%になりました。
蒸発させた水の重さを求めなさい。
解説
食塩の重さは、水を蒸発させても変わりません。食塩の重さは、
180×0.1+10=28(g)
できた食塩水の重さは、
28÷0.2=140(g)
この140gの中に増えた分の食塩10gが含まれるので
140-10=130(g)
よって蒸発させた水の重さは、
180-130=50(g)
答え 50(g)
中学受験 算数の無料問題~図形~
問1
次の図形の面積を求めなさい。
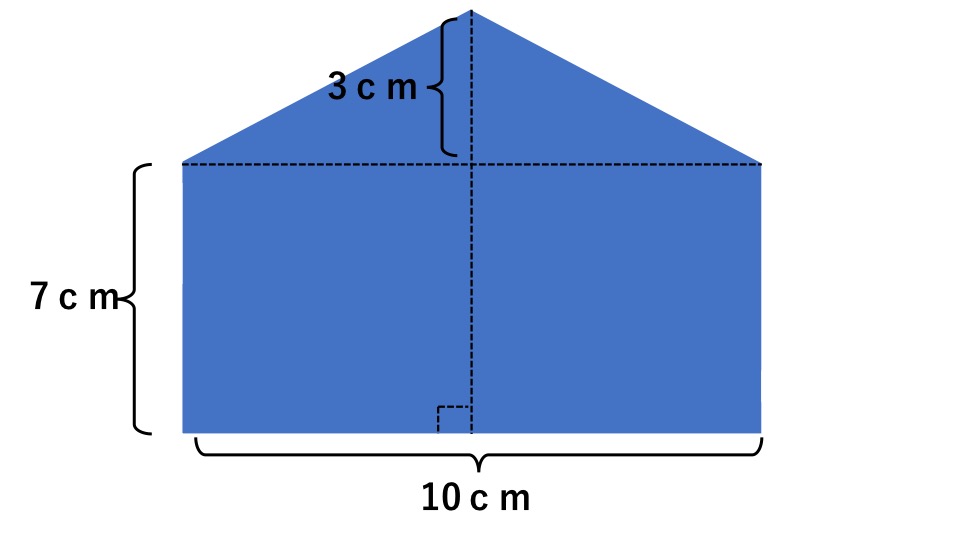
解説
三角形と長方形に分けて面積を求めます。
三角形の底辺は10cm、高さは3cmなので、面積は、
10×3÷2=15(㎠)
長方形のたての長さは7cm、横の長さは10cmなので、面積は、
7×10=70(㎠)
よってこの図形の面積は、
15+70=85(㎠)
答え 85㎠
問2
下の図の色の付いた部分を求めなさい。
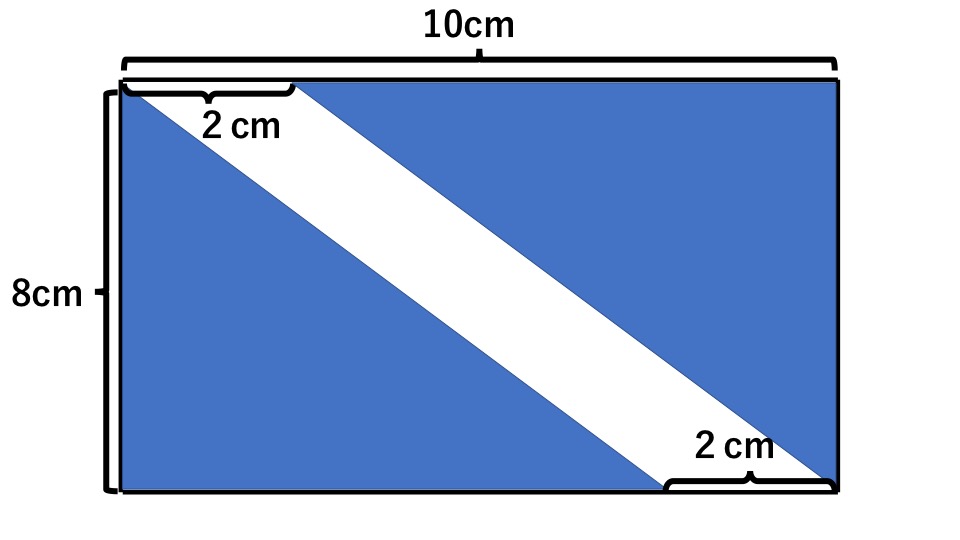
解説
下の図のように、移動したと考えると、
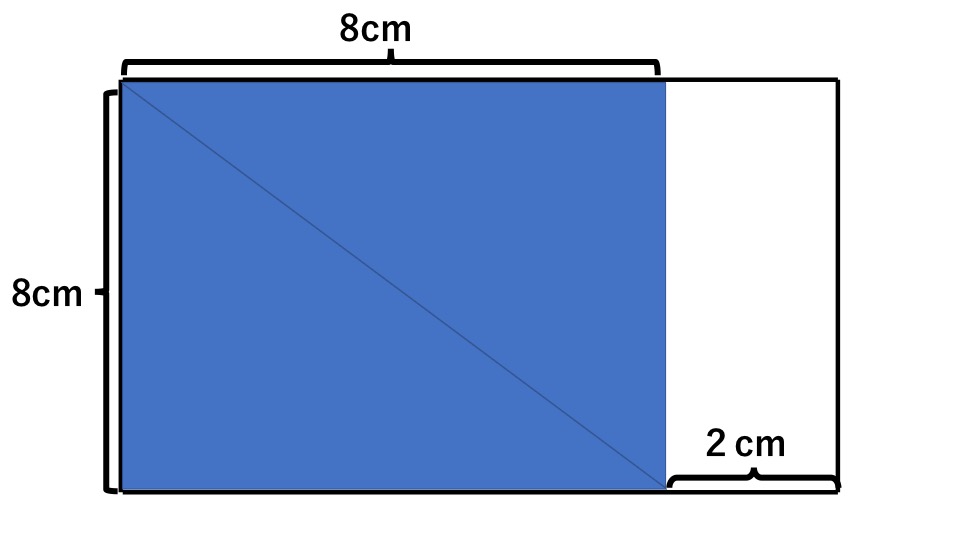
たて8cm、横8cmの正方形になるので、面積は、
8×8=64(㎠)
答え 64㎠
問3
下の図は、大、中、小の3つの円が組み合わさってできた図形です。このとき赤色の部分の面積を求めなさい。円周率は3.14とします。
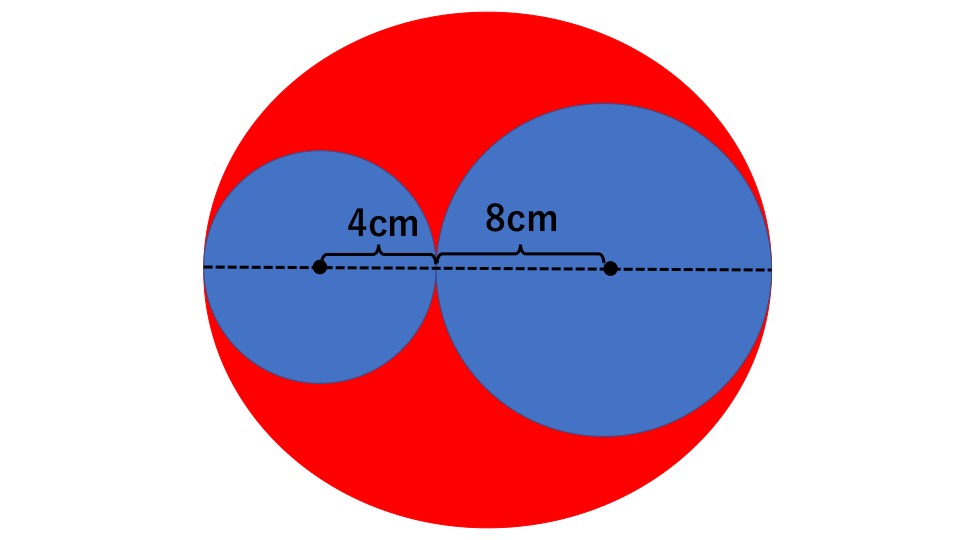
解説
大円の面積から中円、小円の面積の和を引けば求めることができます。
大円の半径は12cmなので面積は、
12×12×3.14=452.16(㎠)
中円の半径は8cmなので面積は、
8×8×3.14=200.96(㎠)
小円の半径は4cmなので面積は、
4×4×3.14=50.24(㎠)
赤色の部分の面積は、
452.16-(200.96+50.24)=200.96(㎠)
よって 答え 200.96㎠
問4
下の図は、底面が半径3cmの円で高さが7cmの円柱です。この円柱の表面積を求めなさい。円周率は3.14とします。
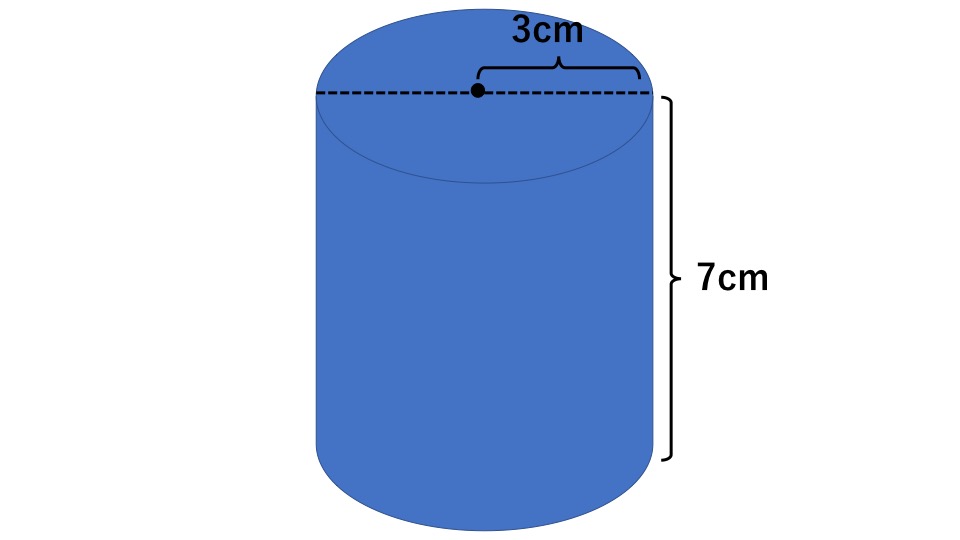
解説
立体図形の表面積を求める際は、展開図を書いて考えます。円柱の展開図は下の図のようになります。
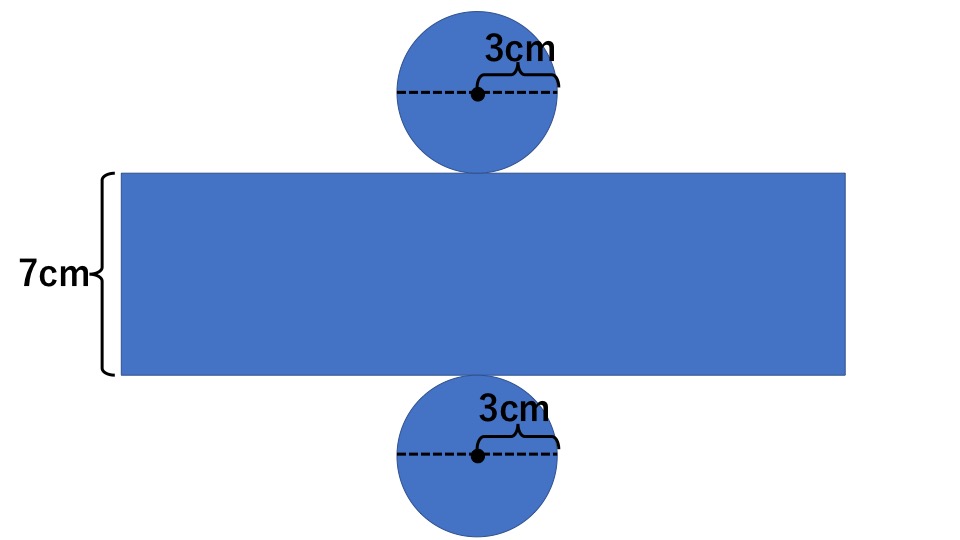
円2つと長方形の和が、円柱の表面積をとなります。
円の半径は3cmなので、円2つ分のの面積は、
3×3×3.14×2=56.52(㎠)
長方形の横の長さは、半径3cmの円周の長さになります。ですので長方形の横の長さは、
3×2×3.14=18.84(㎠)
長方形の面積は、
7×18.84=131.88(㎠)
よって、円柱の表面積は、
56.52+131.88=188.4(㎠)
答え 188.4㎠
中学受験は算数や国語ではなく、「社会」の出来で合否が決まります!
そのため、第一志望に合格したいのであれば、社会を家庭学習でまず最初に固めるのが断トツの近道です!
【社会を最初に固めるべき理由】
● 算数の1点と社会の1点は、総合点で考えれば同じ1点
● 社会は暗記教科で学習センスがいらない!
● 社会は塾任せでは絶対に伸びない、家庭学習で伸ばす!
【短期間で社会の偏差値を上げたい方必見!】
短期間で偏差値を10以上アップさせた受験生多数!社会の偏差値を最速でアップできる社会に特化したスーパー教材を下記のページでご紹介しています!
\ 30日で社会の偏差値がアップ! /
スタディアップの教材はこちら
【たった5分で丸わかり】

